Замок имеет форму квадрата с четырьмя башнями по углам имеется 21 талисман

Как нужно разместить полки для наилучшей защиты замка?

Условие:
Замок имеет форму большого квадрата, составленного из N × N маленьких квадратиков. Внешние квадратики являются башнями, именно они играют основную роль в защите замка от неприятеля. Например, если замок имеет размер 4 × 4, то у него 12 башен (смотрите второй рисунок, башни на нем выделены серым цветом).

Замок охраняют K полков, которые необходимо разместить по башням. В одной башне можно разместить несколько полков, но при этом в каждой башне должен находиться хотя бы один полк, иначе неприятель легко захватит эту башню. Если все башни защищены, то неприятель выбирает для атаки одну из четырех сторон замка, которую защищает наименьшее число полков (то есть суммарное число полков во всех башнях данной стороны квадрата минимально).

Определите, как нужно разместить полки для наилучшей защиты замка.
Я попытался решить эту задачу, посмотрел материал в Инете, но код прошёл не все тесты:

Код я писал пытаясь реализовать такое решение (ответы mail.ru):
Можно по размеру замка узнать количество башен. Для этого из площади замка вычитаем площадь внутреннего двора (квадрат со стороной N — 2).
Замок := N * N
Двор := (N — 2) * (N — 2)
Башни := Замок — Двор

Количество полков K должно быть не меньше количества башен: K >= Башни. Иначе полков не хватит на все башни; жалуемся на несоблюдение условий и завершаем работу.

Первым делом надо разместить в каждой башне по одному полку. Осталось меньше полков: K — Башни.
Сейчас с каждой стороны замка сидит ровно N полков: Охрана = N

Как наиболее эффективно оборонять все стены? Два варианта:
1) поместить полк на стене между углами — тогда один полк будет охранять только одну сторону. Не очень;
2) поместить полк в угловой башне — тогда он будет охранять сразу две стены. Замечательно!

А два полка в противоположных углах будут охранять сразу все стороны. По сути, будет Охрана = N + 1.
Третий полк в углу еще усилит охрану, но только с двух сторон (по-прежнему Охрана = N + 1).
Зато четвертый, напротив третьего, будет охранять оставшиеся две стороны (Охрана = N + 2).

Мы видим простую закономерность: каждые два полка сверх числа башен увеличивают качество охраны на 1 сверх исходного количества полков N с каждой стороны замка.

Таким образом, получаем простую формулу: Охрана := N + (K — Башни) div 2

Я даже понял откуда что берётся в текстовом решении, но переписать на питон не могу

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Источник

Кенгуру олимпиада 2021 ответы и задания 7-8 класс

«Кенгуру» — это массовый международный конкурс-игра для школьников под девизом «Математика для всех». Главная цель конкурса — привлечь как можно больше ребят к решению математических задач, показать каждому школьнику, что обдумывание задачи может быть делом живым, увлекательным, и даже веселым!

Кенгуру 2021 ответы и задания для 7-8 класса

Очередной конкурс «Кенгуру» состоится 18 марта 2021 года. Конкурс проходит один раз в год — в третий четверг марта, проводится он обязательно в школе, подробная информация по ссылке на официальную страницу организатора конкурса: Кенгуру
Ниже представляем первые 10 заданий Кенгуру для 7-8 класса и ответы к ним, обсуждаем остальные задания и ответы в комментариях.

Задачи на 3 балла

Задание 1

В некотором четырехугольнике 1; 2; 2, 8; 5; 7,5 – длины сторон и одной из диагоналей. Какое из этих чисел длина диагонали?

Варианты ответов: (А) 1; (Б) 2; (В) 2,8; (Г) 5; (Д) 7,5.

Наш вариант ответа: (В) 2,8

Задание 2

Какой из следующих символов знаков Зодиака имеет ось симметрии?

Варианты ответов: (А) Стрелец; (Б) Скорпион; (В) Лев; (Г) Рак; (Д) Козерог.

Наш вариант ответа: (А) Стрелец

Задание 3

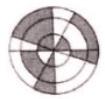
На рисунке показаны три концентрических круга с четырьмя линиями, проходящими через их общий центр. Какой процент фигуры закрашен серым?

Варианты ответов: (А) 30%; (Б) 35%; (В) 40%; (Г) 45%; (Д) 50%.

Наш вариант ответа: (Д) 50%

Задание 4

Сколько есть четырехзначных чисел, цифры в которых идут слева-направо подряд в возрастающем порядке?

Варианты ответов: (А) 5; (Б) 6; (В) 7; (Г) 8; (Д) 9.

Наш вариант ответа: (Б) 6

Задание 5

Если правильно сложить кусочки, получится разность. Чему она равна?

Варианты ответов: (А) -100; (Б) -8; (В) -1; (Г) 199; (Д) 208.

Наш вариант ответа: (А) -100

Задание 6

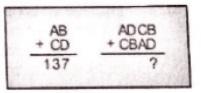
Ученик правильно сложил два двузначных числа, изображенных слева. Какой он должен получить ответ, если сложит числа, изображённые справа? Буквами обозначены цифры от 0 до 9.

Варианты ответов: (А) 13737; (Б) 13837; (В) 14747; (Г) 23737; (Д) 137137.

Наш вариант ответа: (Б) 13837

Задание 7

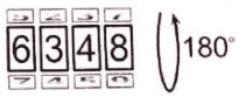
Велосипедный замок состоит из четырех вращающихся колесиков. На каждом колесике установлены цифры от 0 до 9. Переход от одной цифры к следующей или предыдущей получается поворотом колесика на 180 градусов против или по часовой стрелке соответственно. Какой код был установлен на замке велосипедистом, если сейчас на нём код 6348?

Варианты ответов: (А) 0815; (Б) 1893; (В) 1972; (Г) 4892; (Д) 8436.

Наш вариант ответа: (Б) 1893

Задание 8

Боря на 5 см выше Антона, но на 10 см ниже Вани. Гриша на 10 см выше Вани, но на 5 см ниже Димы. Какие из следующих утверждений верно?

(А) Антон и Дима одного роста;
(Б) Антон на 10 см выше Димы;
(В) Антон на 10 см ниже Димы;
(Г) Антон на 30 см выше Димы;
(Д) Антон на 30 см ниже Димы.

Наш вариант ответа: (Д) Антон на 30 см ниже Димы

Задания на 4 балла

Задание 9

Прямоугольная плитка шоколада состоит из равных квадратов. Нил отламывает две полные полосы квадратов и съедает полученные 12 квадратов. Позже Джек отрывает одну полную полосу квадратов от той же плитки и съедает 9 полученных квадратов. Сколько кусочков шоколада осталось в плитке?

Варианты ответов: (А) 72; (Б) 63; (В) 54; (Г) 45; (Д) 36.

Наш вариант ответа: (Г) 45

Задание 10

Банка, заполненная водой на пятую часть, весит 560 г. Та же банка, заполненная на четыре пятых водой, весит 740 г. Какой вес у пустой банки?

Варианты ответов: (А) 60 г; (Б) 112 г; (В) 180 г; (Г) 300 г; (Д) 500 г.

Наш вариант ответа: (Д) 500 г

Задание 11

Площадь большого квадрата 16 см², а площадь каждого маленького 1 см². Какая общая площадь черной фигуры?

Варианты ответов: (А) 3 см; (Б) 3,5 см; (В) 4; (Г) 5,5; (Д) 6.

Наш вариант ответа: (В) 4

Задание 12

5 квадратов расположены, как показано на рисунке. Площадь маленького квадрата равна 1. Чему равно h?

Варианты ответов: (А) 3; (Б) 3,5; (В) 4; (Г) 4,2; (Д) 4,5.

Наш вариант ответа: (В) 4

Задание 13

В викторине 20 вопросов. Каждый правильный ответ оценивается в 7 баллов, при каждом неправильном ответе списывается 4 балла. Если на вопрос не был дан ответ, то количество баллов не меняется. Саша за участие в викторине получил 100 баллов. На сколько вопросов он не ответил?

Варианты ответов: (А) 0; (Б) 1; (В) 2; (Г) 3; (Д) 4.

Наш вариант ответа: (Д) 4

Задание 14

Прямоугольную полоску бумаги 4 х 13 складывают, как показано на схеме.

У двух полученных прямоугольников площади равны P и Q, где P = 2Q. Чему равно х?

Варианты ответов: (А) 5; (Б) 5,5; (В) 6; (Г) 6,5; (Д) 4/2.

Наш вариант ответа: (В) 6

Задание 15

В коробке с фруктами в два раза больше яблок, чем груш. Кристи и Лили разделили их так, чтобы у Кристи было в два раза больше фруктов, чем у Лили. Какое из следующих утверждении всегда верно?

Варианты ответов:
(A) Кристи получила по крайней мере одну грушу
(Б) Кристи получила в два раза больше яблок чем груш
(B) Кристи получила вдвое больше яблок, чем Лили
(Г) у Кристи столько яблок, сколько у Лили груш
(Д) у Кристи было столько груш, сколько яблок у Лили

Наш вариант ответа: (Б) Кристи получила в два раза больше яблок чем груш

Задание 16

У обыкновенной дроби числитель и знаменатель положительны. Числитель этой дроби увеличен на 40 %. На какой процент следует уменьшить ее знаменатель, чтобы новая дробь была вдвое больше исходной дроби?

Варианты ответов: (А) 10%; (Б) 20%; (В) 30%; (Г) 40%; (Д) 50%.

Наш вариант ответа: (А) 10%

Задание 17

На рисунке справа показана пирамида построенная из 20 пушечных ядер. Какое пушечное ядро помечено одной из букв A,B,C,D или E. Имеются четыре пушечных ядра с метками каждого типа. На картинках внизу показаны надписи на ядрах на трёх гранях пирамиды. Какая метка на спрятанном ядре в центре четвёртой грани?

Варианты ответов: (А) A; (Б) B; (В) C; (Г) D; (Д) E.

Наш вариант ответа: (Г) D

Задание 18

Шестизначное число 1ABCDE умножается на 3 и в результате получается шестизначное ABCDE1. Какова сумма цифр этого числа?

Варианты ответов: (А) 24; (Б) 27; (В) 30; (Г) 33; (Д) 36.

Наш вариант ответа: (Б) 27

Задание 19

В коробке находятся только зеленые, красные, синие и желтые фишки. Среди любых 27 фишек, выбранных из коробки, всегда есть хотя бы одна зеленая фишка. Среди любых 25 фишек есть хотя бы одна красная. Среди 22 фишек есть хотя бы одна синяя. И всегда среди любых 17 фишек есть одна желтая. Какое наибольшее количество фишек может быть в коробке?

Варианты ответов: (А) 27; (Б) 29; (В) 51; (Г) 87; (Д) 91.

Наш вариант ответа: (Г) 87

Задание 20

Поверхность футбольного мяча состоит из белых шестиугольников и черных пятиугольников, как показано на рисунке. Всего имеется 12 пятиугольников. Сколько всего шестиугольников?

Варианты ответов: (А) 12; (Б) 15; (В) 18; (Г) 20; (Д) 24.

Наш вариант ответа: (Д) 24

Задание 21

У кубика Рубика 5*5*5 покрасили грани, а потом его распилили на единичные кубики. У скольких маленьких кубиков покрашена хотя бы одна грань?

Варианты ответов: (А) 96; (Б) 98; (В) 100; (Г) 120; (Д) 124.

Наш вариант ответа: (Б) 98

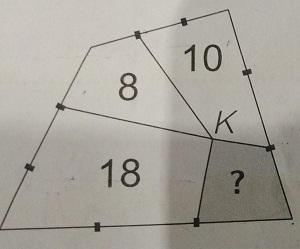
Задание 22

На схеме показан четырехугольник, разделенный на четыре меньших четырехугольника с общей вершиной К. Все стороны большого четырехугольника разделены на три равные части. Числами 8, 10 и 18 обозначены площади соответствующих маленьких четырехугольников. Какова площадь заштрихованного четырехугольника?

Варианты ответов: (А) 4; (Б) 5; (В) 6; (Г) 6,5; (Д) 7.

Наш вариант ответа: (А) 4

Задание 23

В городе 21 рыцарь, которые всегда говорят правду и 2000 лжецов, которые всегда лгут. Волшебник разделил 2020 из этих 2021 человек на 1010 пар. Каждый человек в паре описывал другого человека как рыцаря или лжеца. В результате 2000 человек были названы рыцарями, а 20 человек — лжецами. Сколько было пар из двух лжецов?

Варианты ответов: (А) 980; (Б) 985; (В) 990; (Г) 995; (Д) 1000.

Наш вариант ответа: (В) 990

Задание 24

Пять одинаковых прямоугольных треугольников можно расположить так, чтобы их большие острые углы соприкасались, образуя звезду, показанную на картинке. Также возможно сформировать другую звезду, расположив больше этих треугольников так, чтобы их меньшие острые углы соприкасались. Сколько треугольников нужно, чтобы образовалась вторая звезда?

Варианты ответов: (А) 10; (Б) 12; (В) 18; (Г) 20; (Д) 24.

Наш вариант ответа: (Г) 20

с 18 по 23 января 2021 года уже проводилась Олимпиада Кенгуру для выпускных 4, 9 и 11 класса

Источник