Filosofa.net
Все о философии
Главное Меню
Реклама
Рефераты по философии
Законы науки, способы их открытия и обоснования
4. Динамические и статистические законы
Если основой дихотомического деления законов на теоретические и эмпирические является их различное отношение к опыту, то другая важная их классификация основывается на характере тех предсказаний, которые вытекают из законов. В законах первого типа предсказания носят точно определенный, однозначный характер. Так, если задан закон движения тела и известны его положение и скорость в некоторый момент времени, то по этим данным можно точно определить положение и скорость тела в любой другой момент времени. Законы такого типа в нашей литературе называют динамическими. В зарубежной литературе их чаще всего именуют детерминистическими законами, хотя такое название, как мы увидим ниже, вызывает серьезные возражения.
В законах второго типа, которые получили название статистических, предсказания могут быть сделаны лишь вероятностным образом. В таких законах исследуемое свойство, признак или характеристика относятся не к каждому объекту или индивидууму, а ко всему классу, или популяции в целом. Так, когда говорят, что в данной партии продукции 90% изделий отвечает требованиям стандартов, то это вовсе не означает, что каждое изделие обладает 90% качеством. Само выражение в процентах показывает, что речь здесь идет лишь о некоторой части или пропорции из общего числа изделий, которые соответствуют стандарту. Об отдельном же изделии без дополнительного исследования мы не можем заранее сказать, является оно качественным или нет. Этот элементарный пример достаточно ясно иллюстрирует основную особенность всех статистических законов, предсказания которых относительно отдельных индивидуумов или случаев имеют неопределенный характер. Именно эта неопределенность и заставляет исследователя вводить вероятностные понятия и методы для определения и оценки исхода индивидуальных событий массового случайного типа.
Уже классическая концепция вероятности, нашедшая наиболее полное выражение в трудах П. С. Лапласа, дает возможность оценивать исходы простейших массовых событий случайного характера. В этой концепции вероятность интерпретируется как «отношение числа случаев благоприятствующих к числу всех возможных случаев». При этом, конечно, предполагается, что различные случаи являются равновозможными. Однако такая интерпретация имеет довольно ограниченную область применения. Действительно, равновозможных событий, о которых говорится в вышеприведенном определении вероятности, может просто не быть. Азартные игры, которые исторически явились первой моделью для применения и разработки классической концепции вероятности, специально организованы таким образом, что их исходы являются одинаково возможными, или симметричными. Если, например, игральная кость изготовлена достаточно тщательно, то при ее бросании выпадение любого числа очков от 1 до 6 является одинаково возможным. Поскольку в данном примере имеется шесть равновозможных случаев, благоприятствующим же является какой-то один случай, то его вероятность будет равна 1/6. По такой же схеме подсчитывается вероятность событий, которые можно свести к равновозможным. Иногда это не удается сделать даже в сравнительно простых примерах. Так, если ту же игральную кость изготовить с дефектами, тогда выпадение каждой грани не будет равновозможным. Еще более противоречащими классической концепции являются примеры, взятые из физической, биологической и социальной статистики. Допустим, что вероятность того, что данное вещество из радиоактивного материала будет испускать a-частицу, равна 0,0374. Ясно, что этот результат никак нельзя представить по схеме равновозможных событий. Тогда нам пришлось бы допустить 10000 равновозможных исходов, из них только 374 считались бы благоприятствующими. В действительности же здесь имеются лишь две возможности: либо в следующую секунду вещество испустит частицу, либо нет. Чтобы преодолеть подобные трудности, защитники классической концепции широко использовали так называемый принцип недостаточного основания, или одинакового распределения незнания. Согласно этому принципу, два события считаются равновероятными, если у нас не имеется основания для предположения, что одно из них осуществится скорее, чем другое. Поскольку же в качестве основания зачастую здесь выступало состояние знаний познающего субъекта, то само понятие вероятности лишалось своего объективного значения.
Частотная, статистическая или, как ее иногда называют, эмпирическая концепция вероятности исходит не из наперед заданной, жесткой схемы равновозможных событий, а из действительной оценки частоты появления того или иного события при достаточно большом числе испытаний. В качестве исходного понятия здесь выступает относительная частота появления того или иного признака, характеристики, свойства, которые принято называть событиями в некотором множестве или пространстве событий. Поскольку относительная частота определяется с помощью некоторой эмпирической процедуры, то рассматриваемую вероятность иногда называют еще эмпирической. Это не означает, что само теоретическое понятие вероятности в ее статистической или частотной интерпретации можно определить непосредственно опытным путем. Как мы уже отмечали в предыдущей главе, никакого операционального определения для статистической вероятности дать нельзя, ибо помимо эмпирической процедуры при ее определении мы обращаемся к теоретическим допущениям. В самом деле, осуществив те или иные наблюдения или эксперименты, мы можем точно подсчитать, сколько раз интересующее нас событие встречается в общем числе всех испытаний. Это отношение и будет представлять относительную частоту данного события:
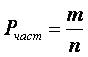
где m означает число появлений данного события, а п — число всех испытаний. Хотя указанное отношение может принимать самые различные численные значения, тем не менее, как показывает практика, для весьма широкого класса случайных массовых событий оно колеблется вокруг некоторого постоянного значения, если число наблюдений или экспериментов будет достаточно велико. Таким образом, тенденция к устойчивости частот обширного класса массовых случайных явлений, обнаруженная на практике, представляет объективную закономерность этих явлений. Абстрактное понятие вероятности как меры возможности наступления события отображает прежде всего этот факт приблизительного равенства относительной частоты вероятности при достаточно большом числе испытаний. Такой подход к вероятности защищается большинством современных специалистов по статистике. Он нашел свое выражение и в широко известном курсе «Математические методы статистики» Г. Крамера. «Всякий раз, — пишет он, — когда мы говорим, что вероятность события Е в эксперименте x равна Р, точный смысл этого утверждения заключается просто в следующем: практически несомненно, что частота события Е в длинном ряду повторений эксперимента x будет приблизительно равной Р. Это утверждение будет называться также частотной интерпретацией вероятности».
Частотный подход к вероятности дает возможность лучше понять специфические особенности статистических закономерностей. Поскольку любое вероятностное утверждение в статистической интерпретации относится не к отдельному событию, а к целому классу однородных или сходных событий, постольку и объяснения и предсказания, полученные с помощью статистических законов, не имеют такого строго однозначного характера, какой присущ динамическим законам. Чрезвычайно важно также отметить, что, в то время как в динамической закономерности необходимость выступает как бы в чистом виде, в статистической закономерности она прокладывает себе дорогу через массу случайностей. В совокупном действии многочисленных случайностей обнаруживается определенная закономерность, которая и отображается статистическим законом.
Как уже отмечалось, статистические закономерности с чисто формальной точки зрения отличаются от закономерностей динамического типа тем, что не определяют значение исследуемой величины достоверным образом, а указывают лишь ее вероятностное распределение. Динамический закон по своей математической форме может быть представлен функциональной связью типа:
 |  |  |  |  |  |  |  |  |  |  |  |  |  |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Название: Законы науки, способы их открытия и обоснования
Дата: 2007-06-09
Просмотрено 42700 раз
Источник
Вероятностные, или статистические законы



Глава 5. Концепция детерминизма и статистические законы
Законы, с которыми мы встречались в классической механике, имеют универсальный характер, т.е. они относятся ко всем без исключения изучаемым объектам. Например, закон всемирного тяготения действителен для всех материальных тел, больших и малых. Отличительная особенность такого рода законов состоит в том, что предсказания, полученные на их основе, имеют достоверный и однозначный характер.
Наряду с ними в науке с середины прошлого века стали все шире применяться законы другого типа. Их предсказания не являются однозначными, а только вероятными. Именно это обстоятельство долгое время служило препятствием для признания их в науке в качестве полноценных законов. Поэтому они рассматривались как вспомогательные средства для обобщения и систематизации эмпирических фактов. Положение коренным образом изменилось после того, как квантовая механика показала, что существование неопределенности коренится в самом фундаменте материи — в мире ее мельчайших частиц, поведение которых можно предсказать лишь с той или иной степенью вероятности.
Вероятностные, или статистические законы
Свое название эти законы получили от характера той информации, которая используется для их формулировки и получения заключения из нее. Вероятностными они называются потому, что заключения, основанные на них, не следуют логически из имеющейся информации, а потому не являются достоверными и однозначными. Поскольку сама информация при этом носит статистический характер, то часто такие законы называют также статистическими, и этот термин получил в науке значительно большее распространение.
Тем не менее, использование термина «вероятность» для характеристики статистических законов более обоснованно с теоретической точки зрения.
Возникает вопрос: о какой вероятности идет речь в данном случае?
В настоящее время существует по крайней мере три интерпретации этого термина. Первая из них связана с классическим периодом развития теории вероятностей, когда вероятность события определялась как отношение числа случаев, благоприятствующих появлению события, к общему числу всех возможных случаев. Такое определение мы встречаем у одного из основоположников классической теории вероятностей — выдающегося французского математика П. С. Лапласа[1]. С помощью такого определения легко подсчитать вероятности, или шансы, появления события в азартных играх, из анализа которых и появилась сама теория. Однако правила азартных игр специально построены таким образом, чтобы шансы игроков были равновозможными, но в природе и обществе равновозможные события встречаются редко. Поэтому для количественной оценки возможности появления тех или иных событий необходимо было найти другую интерпретацию.
Со временем ученым действительно удалось найти ее путем сравнения числа появления исследуемого события к общему числу всех наблюдений. Действительно, чем чаще происходит событие, тем выше вероятности его появления при данных условиях наблюдения. Очевидно, что численное значение вероятности при таком определении зависит от количества наблюдений, т. е. от относительной частоты появления события. Поэтому у чем больше сделано наблюдений, тем точнее будет вычислена и вероятность события. Исходя из этого, некоторые ученые предложили, рассматривать вероятность события как предел его относительной частоты при бесконечном числе наблюдений. Поскольку такое количество наблюдений практически осуществить невозможно, то многие теоретики, а особенно практики, решили определять вероятность как отношение числа появления интересующего события к общему числу всех наблюдений, когда количество последних достаточно велико. Эта величина в каждом конкретном случае должна определяться условиями конкретной задачи, т.е. вероятность Р(А) равна:

где т — число появления интересующего события, а п число всех наблюдений.
Указанное определение вероятности называют также частотным, поскольку в нем фигурирует понятие относительной частоты при длительных наблюдениях. Последние анализируются обычно статистическими методами. Очевидно, что при статистической, или частотной, интерпретации нельзя говорить о вероятности отдельного, единичного события, которое не обладает частотой. Поэтому вероятность при такой интерпретации относится к некоторой группе событий. В предыдущей главе мы упоминали, что волновая функция в квантовой механике определяет параметры будущего состояния системы в «среднем», т. е. не указывает, например, определенное значение его координат, а только тот интервал, в котором они могут находиться. Это обстоятельство часто характеризуют термином «вероятностное распределение».
Частотная, или статистическая, интерпретация вероятности получила наиболее широкое применение в естественных и технических науках, а в последние десятилетия также в социальном и гуманитарном познании. Это осеняется прежде всего тем, что реальные процессы в основном состоят из большого количества элемент, связи между которыми имеют сложный характер щ которых немалую роль играют случайные факторы, от которых нельзя отвлечься, как это делают в классической механике. Тем не менее, и для характеристики таких процессов можно найти некоторые регулярности, которые дают возможность строить вероятностные прогнозы их будущего поведения.
Самое главное применение частотная интерпретация вероятности находит при открытии и анализе статистических законов. Всюду, где мы встречаемся с массовыми случайными или повторяющимися событиями, при тщательней исследовании можно обнаружить, что все они, несмотря на отклонения и разнообразие в своем поведении, обладают определенной регулярностью, а именно: устойчивой относительной частотой. Эта закономерность была давлена еще в античном мире на примере относительны устойчивости количества рождающихся за год мальчиков и девочек. Впоследствии были найдены другие статистические законы в физике, биологии, демографии, страховом деле, социальной статистике и т. д.
Как относились к статистическим законам в классической науке? Признавались ли они в качестве постоянных методов исследования наравне с универсальными законами или считались временными средствами познания’ используемыми для удобства, пока не будут найден подлинные законы?
На этот вопрос можно ответить вполне однозначно: статистические законы не считались подлинными законами, так как ученые прошлого века предполагали, что за ними должны стоять такие же универсальные законы, как закон всемирного тяготения Ньютона, который считался образцом детерминистского закона, поскольку он обеспечивает точные и достоверные предсказания приливов и отливов, солнечных и лунных затмений и других явлений природы.
Статистические же законы признавались в качестве удобных вспомогательных средств исследования, дающих возможность представить в компактной и удобной форме всю имеющуюся информацию о каком либо предмете исследования. Типичным примером может служить информация, получаемая посредством переписи населения. В принципе мы можем получить о каждом гражданине страны все необходимые сведения, но когда они классифицируются по отдельным пунктам, сводятся в отдельные показатели и обобщаются, то работать с такой информацией значительно удобнее и легче. Статистические законы и теоретические обобщения, найденные в физике, биологии, экономике, социологии, праве и других науках, также рассматривались в качестве удобного вспомогательного средства для описания, систематизации и обобщения найденного эмпирического материала. По-видимому, главная причина такого отношения к статистическим законам состояла в том, что заключения их недостоверны, неопределенны, а лишь вероятны в той или иной степени, причем эта степень существенно зависела от количества наблюдений и экспериментов.
В связи с этим подлинными законами считались именно детерминистские законы, обеспечивающие точные и достоверные предсказания. Эта терминология сохранилась до настоящего времени, когда статистические, или вероятностные, законы квалифицируются как индетерминистские, с чем вряд ли можно согласиться. Единственное, что здесь верно, — это качественное различие между двумя типами законов: универсальными и статистическими. В то же время между ними существуют и глубокая общность, и единство, заключающиеся в том, что все они отображают определенные регулярности в природе и обществе. Опираясь на эти регулярности, мы можем успешнее действовать в окружающем нас мире случайностей и неопределенностей, поскольку законы устанавливают некоторые запреты и тем самым уменьшают количество возможных выборов или альтернатив действия.
Отношение к статистическим законам принципиально изменилось после открытия законов квантовой механики, предсказания которых имеют существенно вероятностный характер. Попытка найти некие скрытые параметры, с помощью которых можно было бы свести статистические законы к строго детерминистским законам, подобным законам классической механики, не увенчалась успехом. По-видимому, принцип неопределенности Гейзенберга не дает возможности осуществить это.
Источник



