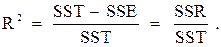Оценка точности уравнения регрессии
Как уже отмечалось, оценки параметров уравнения регрессии
вычисляются по выборочным данным и лишь приближённо равны этим параметрам. В связи с этим появляется необходимость оценить точность как уравнения регрессии в целом, так и его параметров в отдельности. При решении первой задачи используют процедуру дисперсионного анализа, основанную на разложении общей суммы квадратов отклонений зависимой переменной: 
на две составляющие, источниками которых являются отклонения за счёт регрессионной зависимости (SSR) и за счёт случайных ошибок (SSE), причём
Из теории статистики известно, что SST = SSR + SSE или
Аналогичное разложение имеет место и для числа степеней свободы соответствующих сумм:
где dfT = n – 1 – общее число степеней свободы;
dfR = m – число степеней свободы, соответствующее регрессии (m – число независимых переменных в уравнении регрессии);
dfE = n – m – 1 – число степеней свободы, соответствующее ошибкам.
Разделив соответствующие суммы квадратов на степени свободы, получим средние квадраты или дисперсии, которые сравниваются по критерию Фишера для проверки гипотезы о равенстве нулю одновременно всех коэффициентов регрессии против альтернативной: не все коэффициенты регрессии равны нулю. Если нулевая гипотеза отклоняется, то это означает, что уравнение регрессии значимо, в противном случае оно ничего не отражает и не может быть использовано в анализе.
Итак, процедура дисперсионного анализа регрессии состоит в следующем:
рассчитываются суммы квадратов SSR и SSE;
определяются средние квадраты или дисперсии, соответствующие регрессии и ошибкам: MSR = SSR / m и MSE = SSE / n – m – 1;
сравниваются полученные дисперсии на основе критерия Фишера, причём MSR ³ MSE, следовательно 
если F 
/2,m,n—m-1 > F, то уравнение регрессии значимо (не все коэффициенты уравнения регрессии равны нулю), в противном случае – не значимо.
Дисперсионный анализ регрессии удобно проводить в таблице вида:
Таблица 9.1 – Таблица дисперсионного анализа регрессии
| Источник | Сумма квадратов | Степени свободы | Средние квадраты | F-отношение |
| Модель ошибки | SSR SSE | m n – m – 1 | MSR MSE | F=  |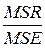
| Общая | SST | n – 1 |
Вернёмся к MSE. Это тоже характеристика точности уравнения регрессии. Этот показатель особого самостоятельного значения не имеет, но участвует в вычислении других показателях точности. Например, корень квадратный из MSE называется стандартной ошибкой оценки по регрессии (Sy,x) и показывает, какую ошибку в среднем получим, если значение зависимой переменной оценивать по уравнению регрессии:
Кроме того, этот показатель в неявном виде участвует в определении коэффициента множественной детерминации (R 2 ):
или после преобразований:
Отсюда следует, что коэффициент множественной детерминации отражает долю вариации изучаемого (результирующего) показателя, обусловленную вариацией за счёт регрессионной зависимости. Коэффициент множественной детерминации иногда выражают в процентах, поэтому, например, если R 2 = 75%, то это означает, что изменение зависимой переменной на 75% объясняется изменением включённых в уравнение регрессии независимых переменных, а остальные 25% – это изменения за счёт неучтённых факторов и случайных отклонений (ошибок).
Корень квадратный из коэффициента множественной детерминации называется коэффициентом множественной корреляции:
который показывает тесноту линейной корреляционной связи между зависимой переменной и всеми независимыми переменными.
Ясно что, R 2 и R изменяются от нуля до единицы и равны единице, если SSE = 0, т.е. связь линейная функциональная и равны нулю, если SST = SSE, т.е. связь отсутствует.
Значимость коэффициента множественной детерминации определяется на основе критерия Фишера:
с m числом степеней свободы числителя и n – m – 1 – знаменателя.
В социально-экономических исследованиях встречается преобразованная формула определения R 2 , имеющая вид:
или в других обозначениях:
,
где Sy,x 2 – выборочная остаточная дисперсия независимого показателя;
Sy 2 – его общая выборочная дисперсия.
Как уже отмечалось, 
– стандартная ошибка оценки по регрессии.
Из определения коэффициента множественной детерминации следует, что он будет увеличиваться при добавлении в уравнение регрессии независимых переменных, как бы слабо ни были они связаны с независимой переменной. Следуя этой логике, для увеличения точности отражения изучаемой зависимости в уравнение регрессии может быть включено неоправдано много независимых переменных. Точность модели при этом увеличится незначимо, а размерность модели возрастёт так, что её анализ будет затруднён. Кроме того, качество оценок при этом ухудшается. Для исключения такого недостатка рассматривают исправленный (на число степеней свободы) коэффициент множественной детерминации:
Этот коэффициент позволяет избежать переоценки независимой переменной при включении её в уравнение регрессии. Если добавление переменной приводит к увеличению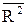 
, то включение её в уравнение регрессии оправдано, в противном случае – нет. Исправленный коэффициент детерминации всегда меньше неисправленного и является несмещённой оценкой для коэффициента множественной детерминации, в то время как неисправленный – завышенный, смещённой оценкой.
Продолжим анализ точности уравнения регрессии. Как уже отмечалось, при проверке значимости уравнения регрессии проверяется гипотеза о том, что все коэффициенты уравнения регрессии равны нулю, против альтернативной – не все коэффициенты регрессии равны нулю. В последнем случае, т.е. если нулевая гипотеза отклонена, встаёт вопрос: какие из коэффициентов равны нулю, а какие значимо отличны от нуля?
Источник
Регрессионный анализ. Уравнение регрессии
Корреляционная связь предполагает зависимость результативного признака от значений факторного признака. Корреляционный анализ устанавливает наличие и тесноту такой связи, но ничего не говорит о её форме и характере изменений. Это является задачей регрессионного анализа. Он представляет собой метод установления функциональной зависимости между условным средним значением результативного (зависимого) признака от факторных (независимых) признаков. При этом предполагается, что результативный признак подчиняется нормальному закону распределения, а факторный признак может иметь произвольный характер распределения.
Термин «регрессия» был впервые использован Фрэнсисом Гальтоном ещё в 1877 году.
Графически регрессия представляет собой теоретическую линию, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию корреляционной связи. Теоретическая линия регрессии отображает изменение средних величин результативного признака y по мере изменения величин факторного признака x при условии полного взаимопогашения всех случайных причин. В идеале сумма отклонений точек поля корреляции от соответствующих точек линии регрессии должна быть равна нолю, а сумма квадратов этих отклонений быть минимальной величиной.
В статистике выделяют различные виды регрессионных моделей.
Парная регрессия представляет собой регрессию между двумя переменными. В качестве примера можно назвать зависимость прибыли предприятия (зависимая переменная) от производительности труда (объясняющая переменная);
Множественная регрессия – регрессия между зависимой переменной у и несколькими причинно обусловленными объясняющими (независимыми, или предсказывающими) х1 х2. хn. Так, имеется множественная регрессия между прибылью предприятия (y) и производительностью труда (x1), объёмом основных фондов (x2), объёмом оборотных средств (x3).
Требования к построению регрессионной модели:
1) совокупность исследуемых данных должна быть однородной и описываться непрерывными функциями;
2) все факторные признаки должны иметь количественное выражение;
3) объём исследуемой статистической совокупности должен быть достаточно большим;
4) должна прослеживаться причинно-следственная связь между изучаемыми явлениями или процессами;
5) территориальная и временная структура статистической совокупности должна быть постоянной.
Этапы регрессионного анализа:
1) построение поля корреляции и выдвижение гипотезы о форме связи;
2) расчёт параметров предполагаемого уравнения регрессии;
3) интерпретация полученных результатов;
4) оценка статистической значимости уравнения регрессии.
Главной задачей регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Главным основанием для выбора уравнения регрессии должен служить содержательный анализ природы изучаемой зависимости, её механизма. Помогает и графическое изображение корреляционного поля, задающего эмпирическую линию регрессии.
Наиболее часто встречающиеся типы функций для парной регрессии:
| Название | Функция |
| Линейная |  |
| Параболическая |  |
| Гиперболическая |  |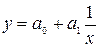
| Показательная |  |
| Степенная |  |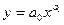
| Логарифмическая |  |
Параметры уравнения регрессии 
, 
и 
находятся при помощи метода наименьших квадратов, разработанного немецким математиком Карлом Фридрихом Гауссом (1777-1855) в 1795 году.
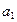
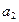
Система нормальных уравнений МНК для линейной парной регрессии имеет следующий вид:
Отсюда можно выразить параметры регрессии:
;
.
Параметр a0 – это постоянная величина в уравнении регрессии. Экономического смысла он не имеет, но в ряде случаев его интерпретируют как начальное значение y, т. е. он показывает усреднённое влияние на результативный признак неучтённых факторов. Если a0>0, то относительное изменение переменной y происходит медленнее, чем изменение переменной x. Если a0
Источник
