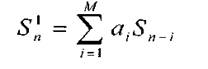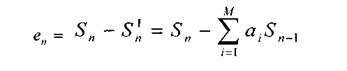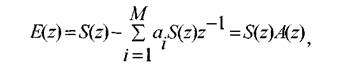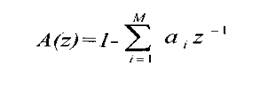Структурная схема анализирующего фильтра линейного предсказания

Вокодеры с линейным предсказанием

Суть кодирования речи на основе метода линейного предсказания (Linear Predictive Coding — LPC) заключается в том, что по линии связи передаются не параметры речевого сигнала, как такового, а параметры некоторого фильтра, в известном смысле эквивалентного голосовому тракту, и параметры сигнала возбуждения этого фильтра.

В качестве такого фильтра используется фильтр линейного предсказания.

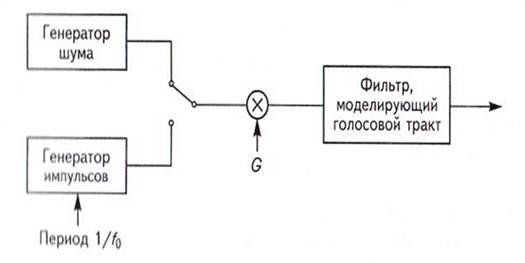
Рисунок 7.9 – Обобщенная схема кодера с линейным предсказанием, где G — коэффициент усиления

f₀ — частота основного тона

Вокодеры с линейным предсказанием (Linear Prediction Coding, LPC) или липредеры основаны на оригинальном математическом аппарате.

Метод линейного предсказания заключается в том, что очередная выборка речевого сигнала S_n с некоторой степенью точности предсказывается линейной комбинацией М предшествующих выборок:

где а_i — коэффициенты линейного предсказания, М — порядок предсказания.

Разность между истинным и предсказанным значениями выборки определяет ошибку предсказания (остаток предсказания):

В результате z-преобразования этого разностного уравнения получаем:

где функция A(z):

Функция A(z) интерпретируется как передаточная характеристика некоторого фильтра, частотная характеристика которого обратна по отношению к частотной характеристике голосового тракта.

Голосовой тракт можно представить как фильтр с регулярно обновляемыми коэффициентами, возбуждаемый каждые 15-30 мс периодическим или шумоподобнымсигналом. Речевой кодер производит синтез фильтра, моделирующего голосовой тракт речевого сигнала — устанавливает тип возбуждения (шум или последовательность импульсов) и его период.

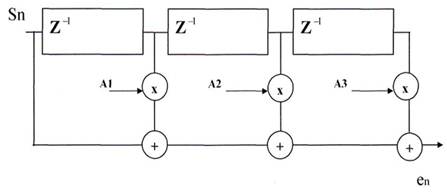
При подаче речевого сигнала на вход инверсного фильтра на выходе фильтра получается сигнал возбуждения, подобный сигналу возбуждения на входе фильтра голосового тракта.

Рисунок 7.10 – Схема инверсного фильтра

Порядок предсказания выбирается из условия компромисса между качеством передачи речи и пропускной способностью линии связи; практически М берется порядка 10.

Значения коэффициентов предсказания, постоянные на интервале кодируемого сегмента речи (на практике длительность сегмента составляет 20 мс), находятся из условия минимизации среднеквадратического значения остатка предсказания на интервале сегмента.

Процедура кодирования речи в методе линейного предсказания сводится к следующему:

1) оцифрованный сигнал речи нарезается на сегменты длительностью 20 мс (160 выборок по 8 бит в каждом сегменте);

2) для каждого сегмента оцениваются параметры фильтра линейного предсказания и параметры сигнала возбуждения;

3) в качестве сигнала возбуждения в простейшем случае может выступать остаток предсказания, получаемый при пропускании сегмента речи через фильтр линейного предсказания с параметрами, полученными из оценки для данного сегмента;

4) параметры фильтра и параметры сигнала возбуждения кодируются по определенному закону и передаются в канал связи.

Рисунок 7.11 Кодирование речи на основе метода линейного предсказания

Процедура декодирования речи заключается в пропускании принятого сигнала возбуждения через синтезирующий фильтр известной структуры, параметры которого переданы одновременно с сигналом возбуждения. Сигнал на вход анализирующего фильтра поступает непосредственно с выхода АЦП, а выходной сигнал синтезирующего фильтра попадает на вход ЦАП. Приведенное описание процессов кодирования и декодирования речи не является исчерпывающим, оно объясняет лишь принцип действия кодека. Практические схемы заметно сложнее, и это связано в основном со следующими двумя моментами.

Во-первых, речевой сигнал обладает двумя видами внутренних корреляционных связей, кратковременной и долговременной избыточностью, поэтому в подавляющем большинстве современных речевых кодеков используется два предсказателя: кратковременный (SHORT-TERM) и долговременный (LONG-TERM). Первый предсказатель (STP), учитывающий кратковременную избыточность РС, связан с корреляциями между близко расположенными отсчетами сигнала и определяет огибающую спектра. Его порядок обычно бывает 6÷10. Второй, долговременный, предсказатель (LTP) определяет тонкую структуру РС и связан с корреляцией двух отрезков сигнала между собой, реально — двух соседних периодов основного тона (ОТ). Период основного тона речиизменяется в широких пределах. На практике обеспечивается формирование частоты ОТ в пределах 57 ё 500 Гц , что соответствует изменению периода от 2 до 17,5 мс.

Сочетание двух предсказателей с разными характеристиками позволяет в значительной мере устранить остаточную избыточность и приблизить остаток предсказания по своим статистическим характеристикам к белому шуму. При этом на приемную сторону передаются остаток предсказания и коэффициенты обоих (STP и LTP) предсказаний.

Во-вторых, использование остатка предсказания в качестве сигнала возбуждения оказывается недостаточно эффективным, так как требует для кодирования слишком большого числа бит. Поэтому практическое применение находят более экономичные (по загрузке канала связи, но отнюдь не по вычислительным затратам) методы формирования сигнала возбуждения.

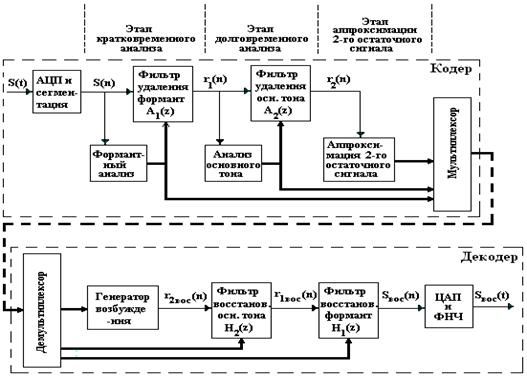
Рассмотрим структурную схему вокодера с линейным предсказанием более подробно. На подготовительном этапе выполняют аналого-цифровое преобразование РС и сегментацию цифрового потока: для последующей обработки выбирают отсчеты сигнала на интервале длительностью 20 мс, что при F_д = 8 кГц обеспечивает число обрабатываемых отсчетов равное 160. После сегментации отсчетов РС в кодере последовательно выполняются следующие три процедуры:

1. кратковременный (формантный) анализ с использованием процедуры линейного предсказания, в результате чего получают первый остаточный сигнал r₁(k);

2. долговременный анализ с использованием линейного предсказания для определения параметров ОТ, в результате чего получают второй остаточный сигнал r₂(k), близкий по своим характеристикам к шумовому, поскольку между отсчетами этого сигнала корреляция мала;

3. аппроксимация второго остаточного сигнала с целью формирования сигнала возбуждения.

В первой процедуре оценку текущего отсчета Ś(k) определяют как сумму P предшествующих отсчетов. При формантном анализе порядок предсказания P выбирают равным 8 – 12. Определение коэффициентов предсказания a_pi фильтра-анализатора производят в блоке формантного анализа из условия минимизации среднеквадратичного значения ошибки предсказания (т.е. первого остаточного сигнала) на интервале сегмента.

Вычисленные значения коэффициентов предсказания используют в фильтре удаления формант кодера, на выходе которого получают сигнал, свободный от квазипериодических составляющих – формант; его называют первым остаточным сигналом. Информацию о формантах несут переданные на приемный конец параметры фильтра a_pi, либо связанные с ними коэффициенты частичной корреляции (коэффициенты отражения). Иногда используют функции от коэффициентов отражения — так называемые логарифмические отношения площадей.

Во второй процедуре с учетом того, что основной тон характеризуется всего двумя параметрами, — амплитудой и периодом, передаточная функция фильтра удаления ОТ A₂(z) описывается более простым выражением

,

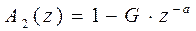
где G — единственный коэффициент предсказания, характеризующий амплитуду основного тона. Задержка a определяет период основного тона, ее значение обычно заключается в пределах от 20 до 160 интервалов дискретизации сигнала, что соответствует диапазону частот основного тона 50 — 400 Гц. Известно, что значение основного тона для разных голосов может изменяться почти в 10 раз — от 2 до 18 мс. Это обстоятельство создает немало трудностей при оценке ОТ, так как слух очень чувствителен к его искажениям. Методов измерения ОТ известно очень много и, вместе с тем, метод, не требующий чрезмерной задержки, пока не появился.

Несмотря на относительную простоту выражения, анализ и удаление ОТ является более сложной процедурой по сравнению с формантным анализом. Это обусловлено существенно большим периодом ОТ и сложностью выявления корреляции между отсчетами на большом временном интервале. Кроме того, период и амплитуда ОТ очень важны для точного восстановления речи. Именно поэтому на этапе долговременного анализа сегмент речи разделяют на 4 подсегмента. Каждый подсегмент имеет длительность 5 мс и содержит 40 отсчетов. Значения G и a определяют для каждого подсегмента по отдельности. Найденные параметры G и a используют в фильтре удаления основного тона. Их также передают на приемный конец в декодер, где используют при синтезе речевого сигнала.

Рисунок 7.12 Структурная схема липредора

Решаемая задача третьей процедуры — при минимальном объеме информации о сигнале возбуждения обеспечить приемлемое качество восстановленного сигнала. Для достижения этого обработку второго остаточного сигнала производят отдельно для каждого подсегмента из 40 отсчетов. Суть аппроксимации состоит в том, что второй остаточный сигнал моделируют в виде определенного числа импульсов на интервале подсегмента.

Переданные по каналу связи параметры аппроксимации второго остаточного сигнала, параметры основного тона G и a, коэффициенты формантного фильтра a_pi поступают на соответствующие блоки декодера (рисунок 7.12). В любом случае по каналу связи вместо самой речи передают так или иначе выделенные и квантованные параметры кратковременного и долговременного предсказания, интервал и усиление ОТ, параметры возбуждения. В декодере ЛП по принятым параметрам восстанавливают сигнал возбуждения, пропускают его через синтезирующий фильтр и восстанавливают речь.

Синтез сигнала начинают с восстановления второго остаточного сигнала, выполняемого генератором возбуждения. Восстановленный сигнал r_2вос(k) несколько отличается от второго остаточного сигнала в кодере из-за погрешности аппроксимации.

Восстановленный второй остаточный сигнал пропускают через фильтр восстановления основного тона, передаточную характеристику которого H₂(z) устанавливают обратной характеристике фильтра удаления основного тона кодера:

.

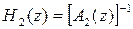
На выходе этого фильтра получают восстановленный первый остаточный сигнал r_1вос(k), который включает основной тон. Наконец, фильтр восстановления формант с передаточной функцией H(z) восстанавливает формантные составляющие сигнала.

Восстановленный сигнал S_вос(n) достаточно близок к исходному сигналу на входе кодера S(n). Выполнив цифро-аналоговое преобразование и пропустив сигнал через ФНЧ, получают восстановленный аналоговый сигнал.

Все процедуры обработки сигнала в кодере и декодере выполняются цифровыми методами. Кодер и декодер реализуют на высокопроизводительном сигнальном процессоре. Показанные на рисунке 7.12 модули липредора фактически являются блоками программного обеспечения.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Применение модели линейного предсказания для анализа стохастических сигналов

Рубрика: 2. Электроника, радиотехника и связь

Статья просмотрена: 2873 раза

Библиографическое описание:

Кагановский, Ю. Д. Применение модели линейного предсказания для анализа стохастических сигналов / Ю. Д. Кагановский. — Текст : непосредственный // Технические науки: традиции и инновации : материалы I Междунар. науч. конф. (г. Челябинск, январь 2012 г.). — Челябинск : Два комсомольца, 2012. — С. 12-14. — URL: https://moluch.ru/conf/tech/archive/6/1596/ (дата обращения: 07.07.2021).

В начале нового тысячелетия в России начался активный переход на цифровые стандарты связи. Региональные и общегосударственные операторы отказываются от устаревшего аналогового оборудования АТС в пользу намного более производительного и компактного, цифрового. В это время для специалистов в области телекоммуникаций стоит первоочередная задача проектирования удобных, производительных и экономически выгодных систем связи. Ключевым моментом в реализации этой задачи является достижение как можно большего количества подключенных к сети абонентов при как можно меньшем количестве сложного оборудования и высоком качестве связи. Под качеством связи зачастую принято понимать качество речи, которую абонент слышит в трубке телефона. Для количественного описания процессов формирования и передачи рече­вых сигналов было предложено много различных моделей. Можно, однако, с уверенностью сказать, что ни одна из них не позволяет объяснить все харак­теристики человеческой речи. Такая модель, в силу своей большой сложности, вероятно, и не потребуется. Во всех практических случаях при выборе мате­матической модели стремятся обеспечить ее минимальную сложность при мак­симальной точности. Одной из наиболее удачных моделей акустического ре­чевого сигнала является линейная модель, разработанная Фантом. Эта модель далее будет называться моделью речеобразования.

В последние годы в задачах моделирования речевых сигналов широко применялись математические методы линейного предсказания. Модель на ос­нове линейного предсказания может быть легко преобразована в модель ре­чеобразования. Важным ее достоинством является относительная простота оценки параметров, использующей линейные процедуры обработки сигнала. На основе данной модели строятся LPC -вокодеры, или т.н. липредеры. В подобных вокодерах используются алгоритмы линейного предсказания, с помощью которых при анализе в передающем устройстве определяются коэффициенты предсказания, а в приемном устройстве на основе этих коэффициентов с помощью рекурсивного цифрового фильтра синтезируется эквивалент голосового тракта. Эти системы получили наибольшее распространение в мире и являются одними из самых перспективно развивающихся.

Основной проблемой, возникающей при анализе недетерминированных сигналов разнообразной природы (речевых, медицинских, сейсмических, геофизических при поиске и разработке месторождений полезных ископаемых) и динамических систем, является определение их временных и частотных характеристик, поскольку любой недетерминированный сигнал и динамическая система в принципе являются нелинейными объектами, что чрезвычайно усложняет их анализ.

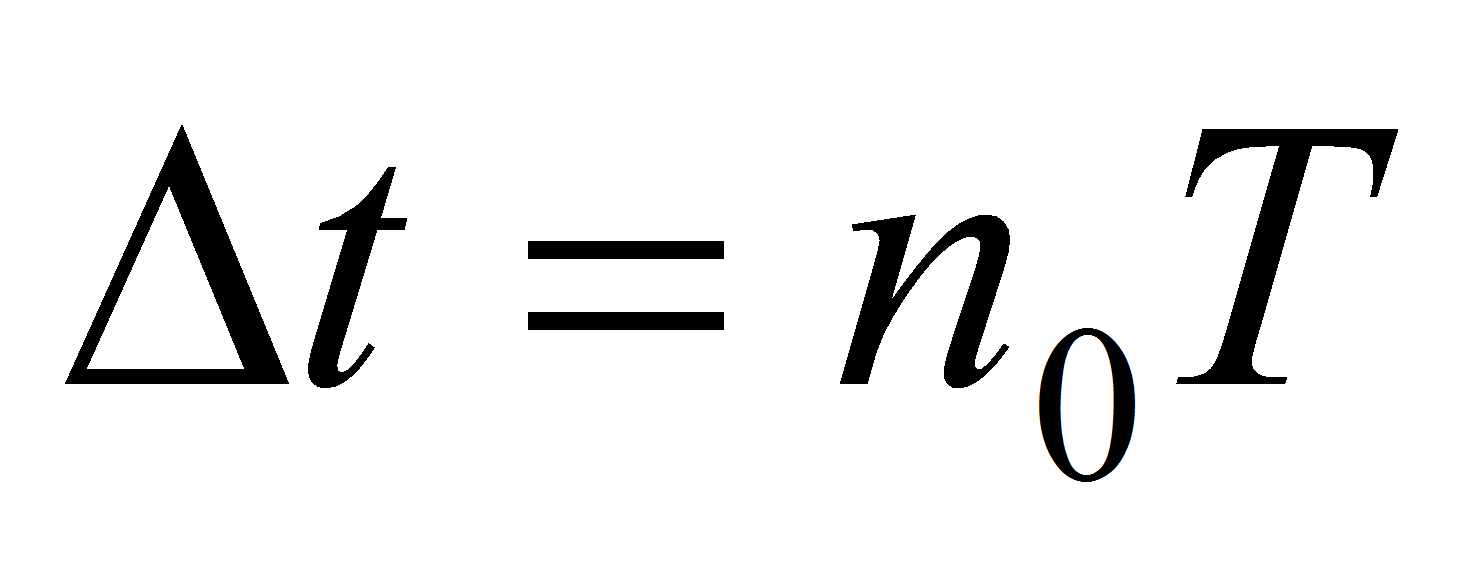
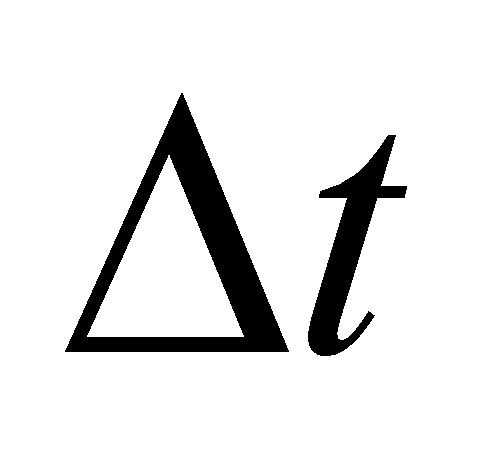
Однако всегда можно выделить некоторый временной интервал ( Т – период дискретизации), на котором параметры объекта изменяются не слишком сильно. Такой интервал называют интервалом квазистационарности, а параметры объекта на этом интервале считаются постоянными. Отрезок сигнала x ( nT ) на интервале называется кадром.

Если построить достаточно точную параметрическую модель объекта для интервала квазистационарности, то ее можно использовать в самых различных случаях, в том числе, например, в системах управления и сжатия данных. Самыми простыми являются линейные модели, которые легко описываются в терминах передаточных функций [2, с. 125]. 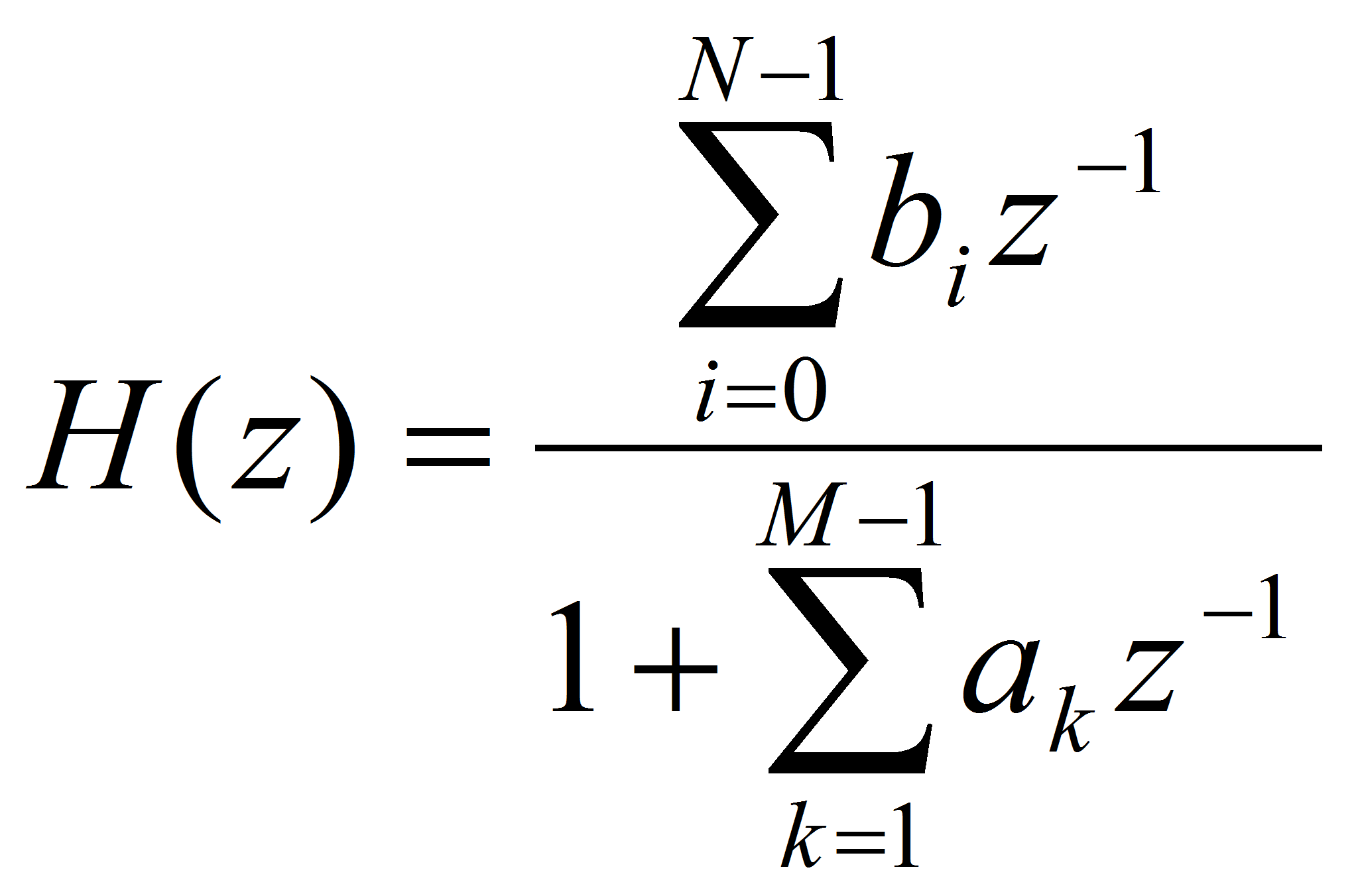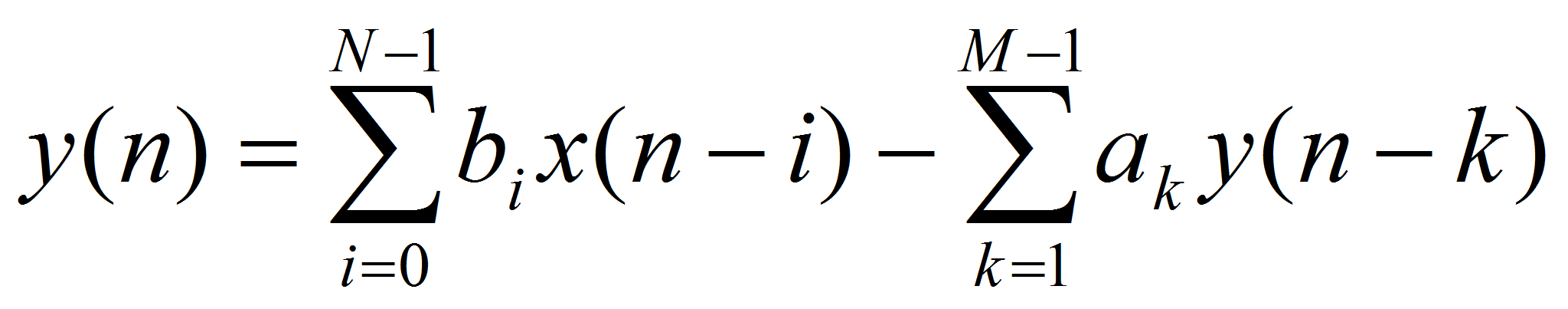Наиболее полной в указанном смысле моделью представляется рекурсивная система порядка К=М – 1, описываемая передаточной функцией: или соответствующим разностным уравнением: .

Наиболее широко в настоящее время применяется полюсная модель, числитель передаточной функции (левая сумма в разностном уравнении) которой содержит только один коэффициент b 0 .

Пусть на некоторую линейную модель системы с передаточной функцией H ( z ) воздействует сигнал возбуждения x ( n ) , а на ее выходе формируется сигнал y ( n ) . Параметры системы, т.е. коэффициенты передаточной функции, неизвестны. Требуется найти коэффициенты < a k >, такие, чтобы на интервале квазистационарности выполнялось равенство: 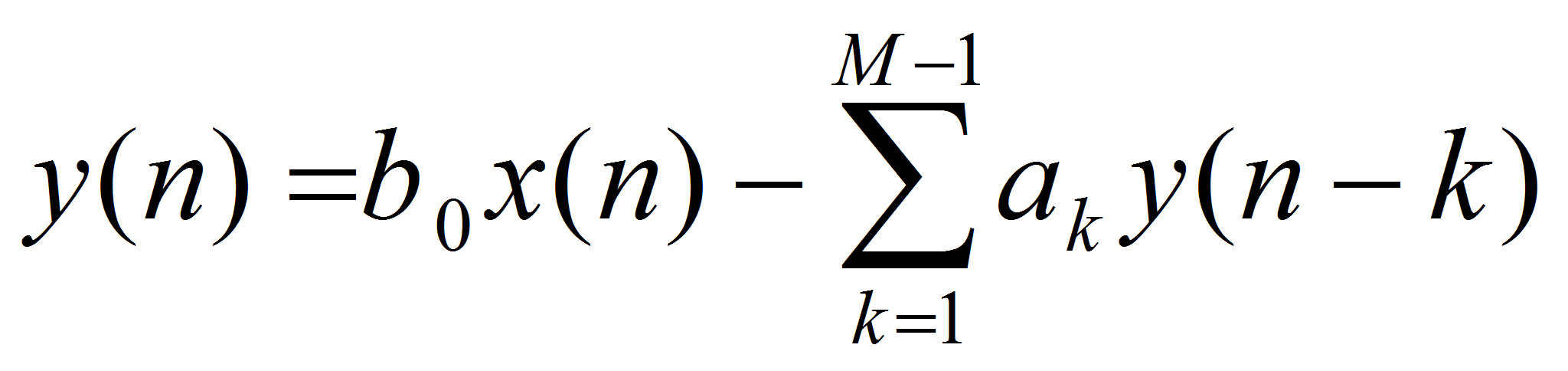при условии, что сигнал возбуждения x ( n ) неизвестен. Фактически необходимо предсказать текущее значение сигнала y ( n ) по его известным предыдущим отсчетам. Таким образом, можно сделать вывод, что линейное предсказание – это вычислительная процедура, позволяющая по некоторой линейной комбинации L предшествующих взвешенных отсчетов недетерминированного сигнала предсказать (с определенной точностью) будущее значение отсчета.

Рис. 1. Линейная модель системы

Практическая важность линейного предсказания состоит в оценке спектра исследуемого сигнала на его отрезке (кадре) длиной в L отсчетов, а с точки зрения фильтрации – в получении рекурсивного адаптивного фильтра порядка K = M – 1 на участке квазистационарности, т.е. на том временном отрезке длительностью LT ( T – период дискретизации), где коэффициенты фильтра остаются постоянными. Итогом решения задачи линейного предсказания будет являться получение коэффициентов адаптивного фильтра, АЧХ которого с хорошей степенью приближения совпадает с формой спектра сигнала в кадре [3, с. 46]. Задача линейного предсказания сформулируем следующим образом. На выходе некоторой системы наблюдается сигнал y ( n ) ; известно, что эта система: 1. 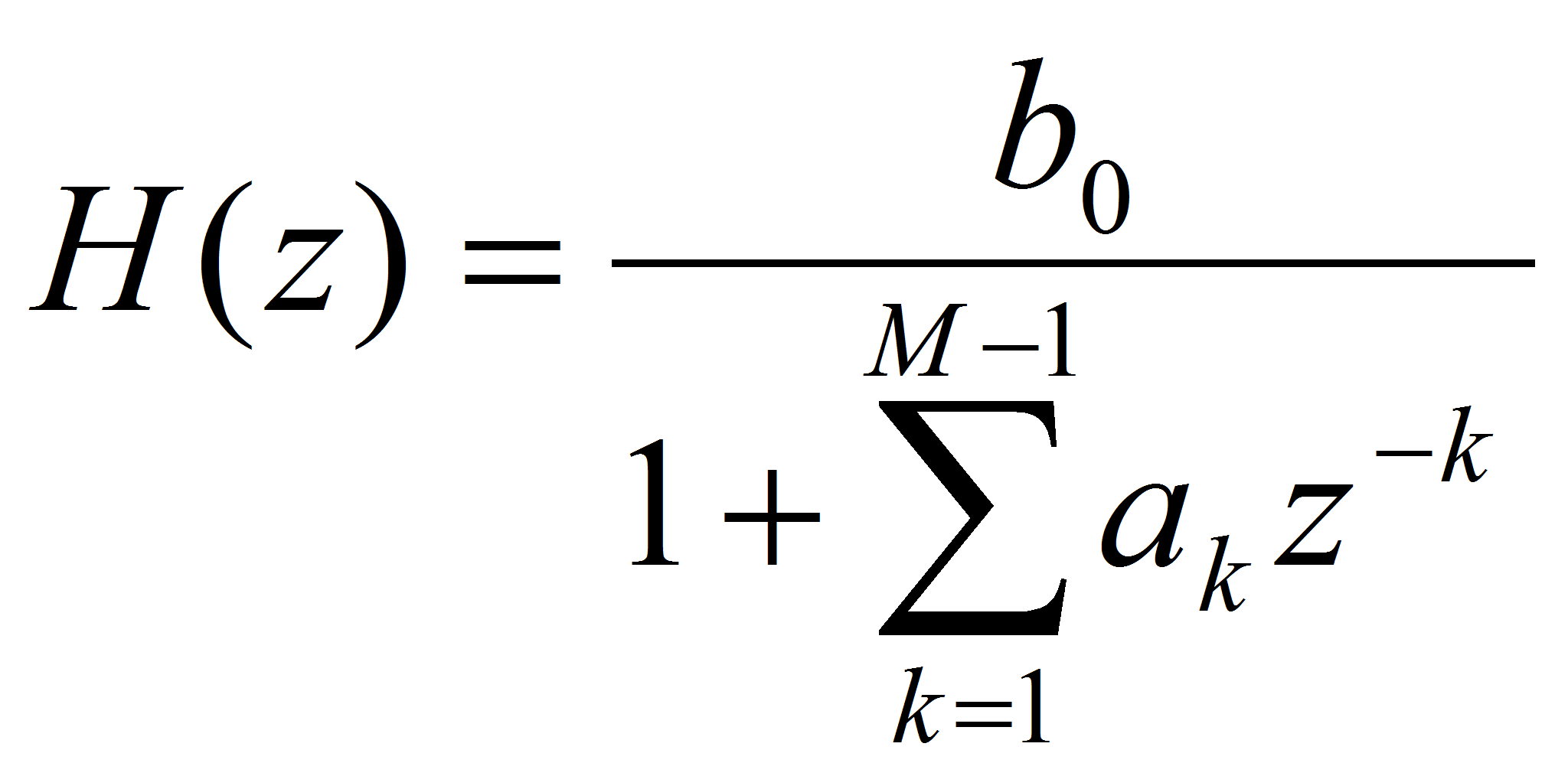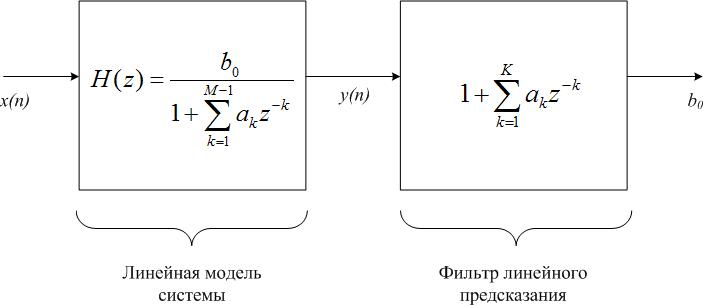Полюсного типа с передаточной функцией вида: , 2. Имеет порядок K = M – 1, 3.Сигнал возбуждения не наблюдается. Требуется найти коэффициенты < a k >. Подход к решению поставленной задачи состоит в следующем. Согласно формуле передаточной функции, представленной выше, сигнал y ( n ) определяется выражением: .

Рис. 2. Решение задачи линейного предсказания
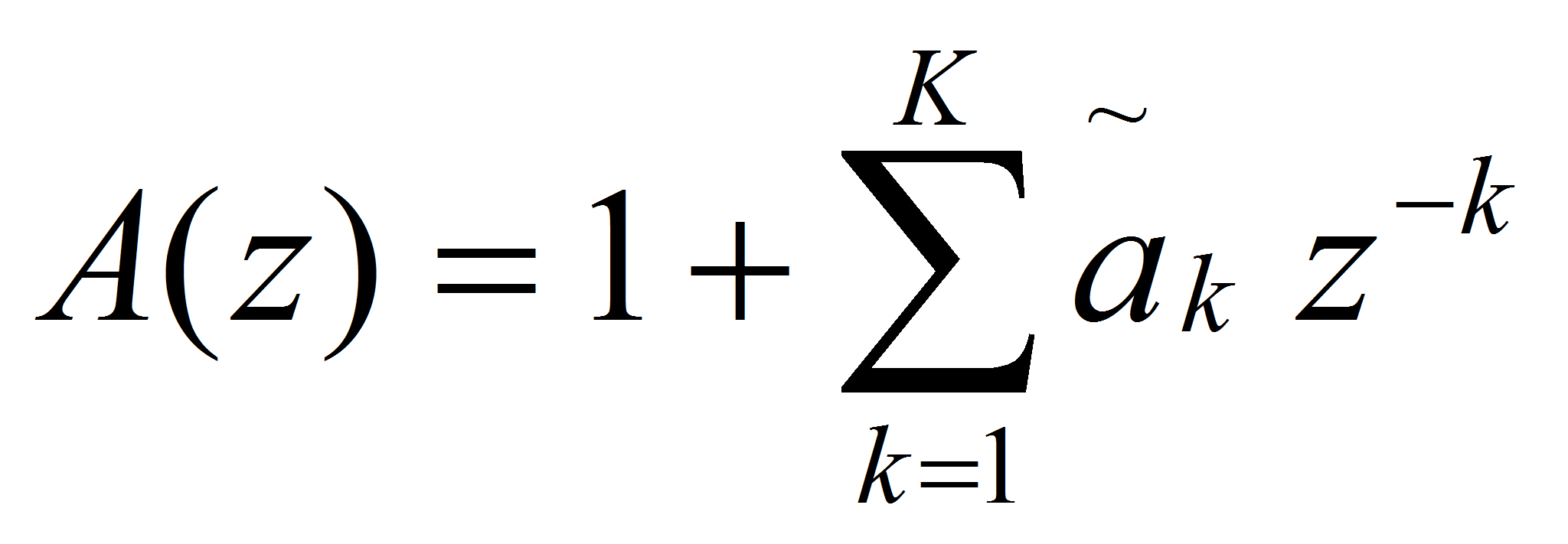
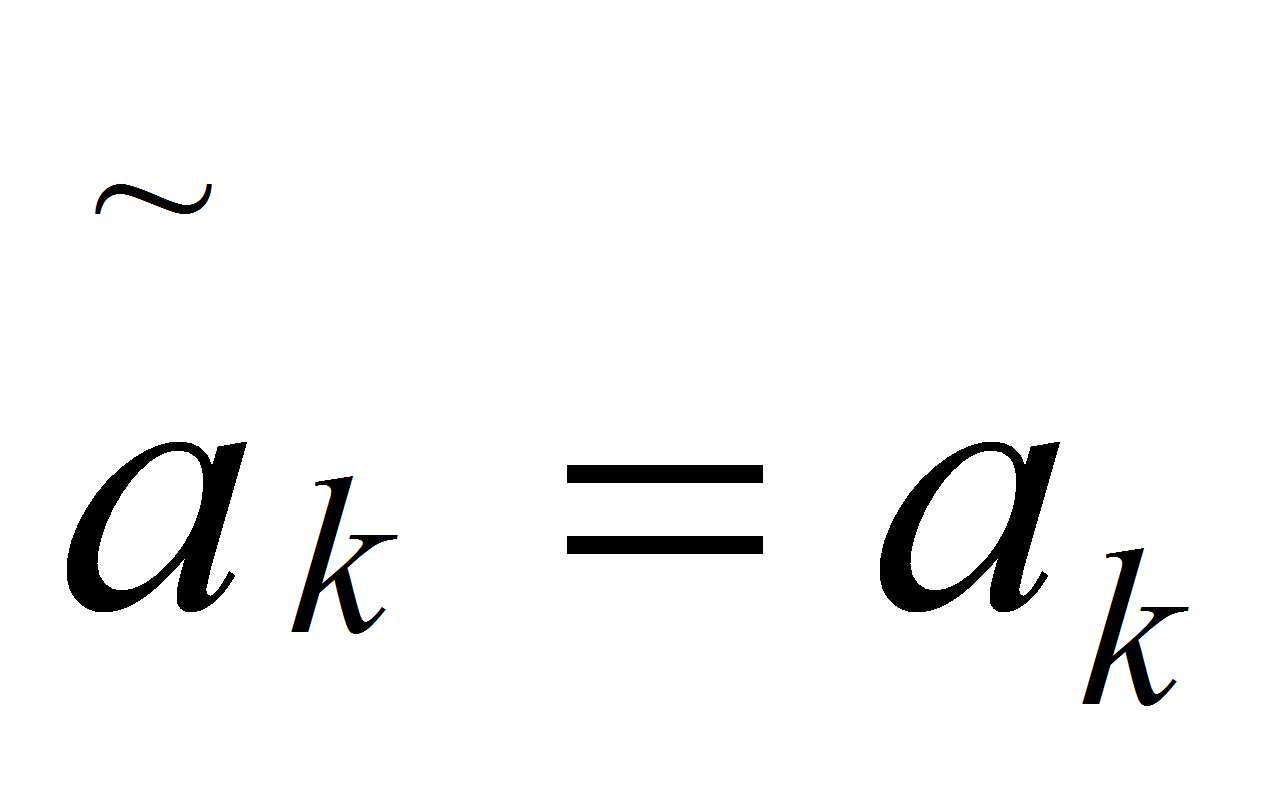
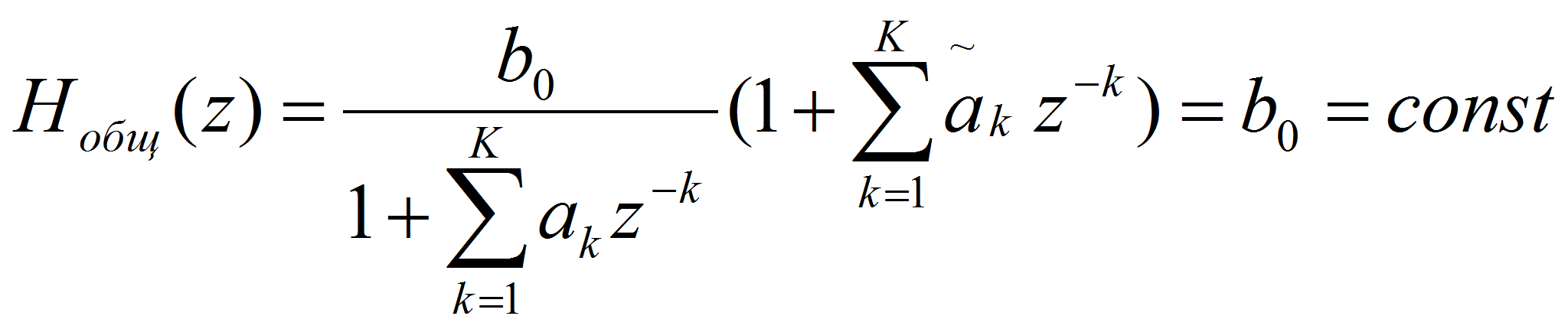
Включим последовательно с искомой системой КИХ-фильтр с передаточной функцией: , коэффициенты которой . Передаточная функция образованной системы получит вид: .

КИХ-фильтр с передаточной функцией A ( z ) называется фильтром линейного предсказания, или фильтром-предсказателем, его порядок K – порядком предсказания, а его коэффициенты — коэффициентами линейного предсказания [1, с. 84].

В действительности коэффициенты будут отличаться от точных значений a k , поэтому предсказываемое значение сигнала будет отличаться от точного y ( n ) на величину ошибки предсказания (при n > 0): , которую называют остатком.

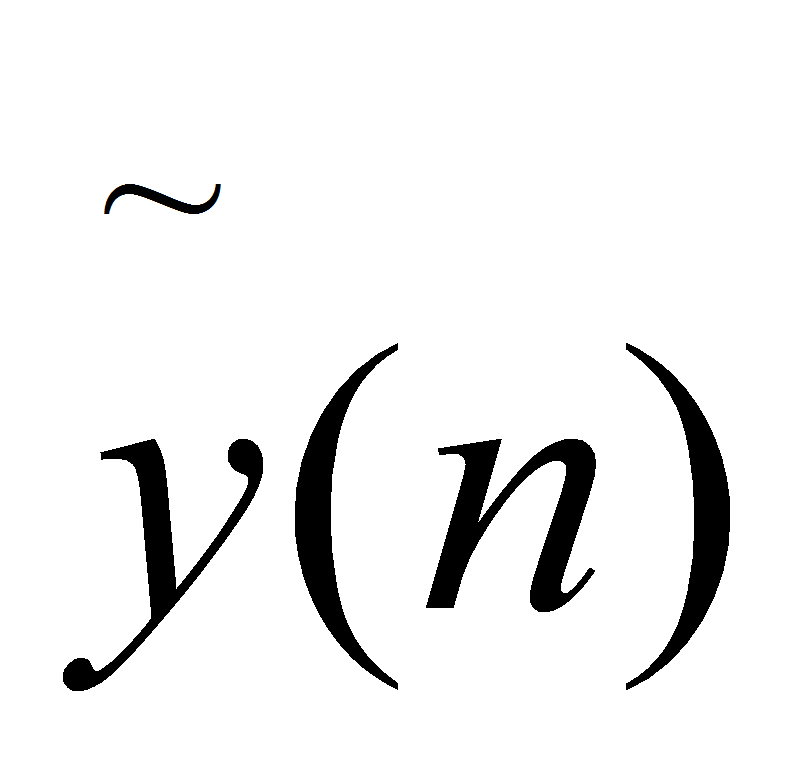
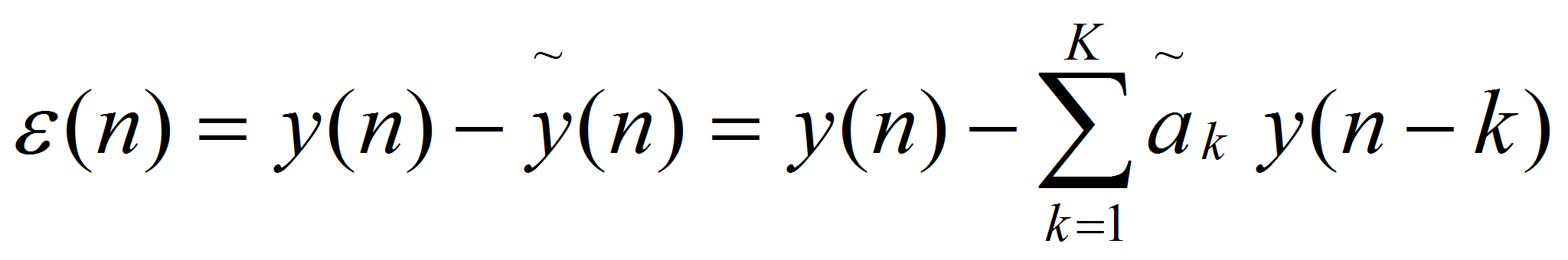
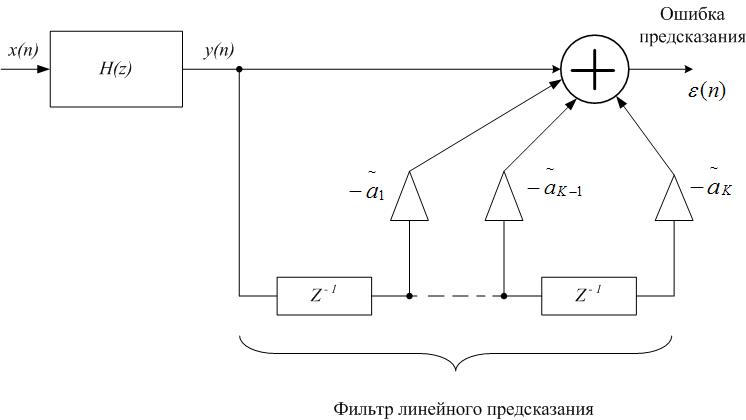
Рис. 3. Структурная схема системы с фильтром-предсказателем

Схема решения задачи линейного предсказания и формулы передаточной функции показывают, что передаточная функция построенной системы с точностью до коэффициента b 0 представляет собой обратную передаточную функцию (а потому и частотную характеристику) фильтра-предсказателя: 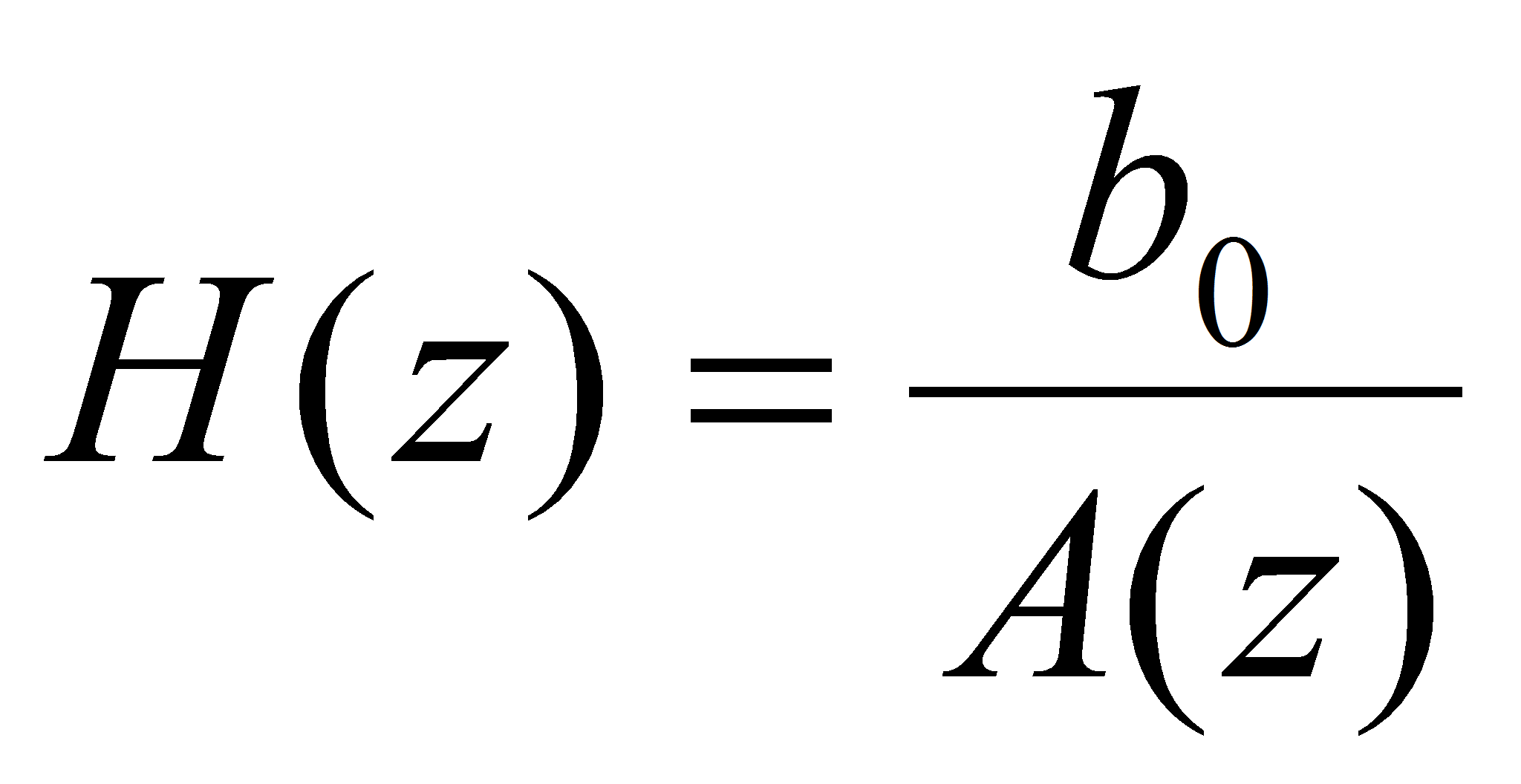, откуда видно, что линейное предсказание – это способ оценки спектра сигнала на выходе линейного тракта с неизвестными параметрами.

Таким образом, данный алгоритм применения линейного предсказания можно применять к различного рода недетерминированным сигналам, в том числе и к речевым, что открывает широкие возможности применения данного предсказания в области компрессии речевых данных.

Рабинер Л., Гоулд Б., Теория и применение цифровой обработки сигналов / Пер.с англ.; Под ред. Ю.И. Александрова. – М.: Мир, 1978. – 848 с.

Сергиенко А.Б. Цифровая обработка сигналов. 2 – изд. – СПб.: Питер, 2006. – 608 с.

Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра. Пер с англ. – М.: Радио и связь, 2000. – 253 c .

Похожие статьи

Расчет нелинейностей аналого-цифрового преобразователя

линейное предсказание, передаточная функция, интервал квазистационарности. О непараметрическом алгоритме моделирования нелинейных.

Методы распознавания речи | Статья в журнале «Молодой ученый»

линейное предсказание, задача, решение этой, речевой сигнал, последовательность наблюдений, нейронная сеть, модель, коэффициент, исходный сигнал, скрытая марковская модель.

Управление линейной динамической системой в условиях.

О выборе параметрической модели в задаче непараметрической. В настоящей работе рассматривается задача получения передаточной функции объекта управления по математической модели замкнутой линейной динамической системы с целью настройки.

О непараметрическом регуляторе для линейных динамических.

Рис.4 Непараметрическая оценка переходной характеристики системы. замкнутая система, передаточная функция, переходная характеристика, задающее воздействие, весовая функция, входной сигнал.

Декомпозиция линейной модели квадрокоптера

управляющий сигнал, одинаковая величина, пространство состояний, мотор, синтез системы управления, линеаризация системы, математическая модель, линейная система, горизонтальное положение, система.

Последовательности с идеальной периодической.

Применение модели линейного предсказания для анализа. Рис. 1. Линейная модель системы. Практическая важность линейного предсказания состоит в оценке спектра исследуемого сигнала на его отрезке.

Реализация модели приёмника 4-позиционного.

Описание характеристик моделируемой системы. Когда речь идет о производительности

Для этого рассмотрим математическую модель для сигнала на входе приемника. Пусть канал задерживает переданные сигналы и искажает посредством аддитивного гауссовского шума.

Использование пассивного эксперимента при идентификации.

передаточная функция, график сигналов, активный эксперимент, пассивная идентификация, основная форма модуля, настроечный параметр регулятора, математическое описание, входной сигнал системы.

Выделение границ фонем речевого сигнала с помощью.

Предварительная обработка речевых сигналов для системы.

Построение концептуальной модели сингулярного эстиматора. 1) Разложение исходного речевого сигнала в спектр квазигармонических компонент (задача 1).

Источник