Предсказание временных рядов с помощью нейронных сетей

ПРИМЕНЕНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ ФИНАНСОВЫХ ВРЕМЕННЫХ РЯДОВ

Авторы: Е.А. Ефремова, Е.В. Дунаев

Описание: В статье рассмотрены некоторые аспекты и особенности использования нейронных сетей для прогнозирования финансовых временных рядов с целью получения прибыли.

Введение.

Предсказание финансовых временных рядов – необходимый элемент любой инвестици- онной деятельности. Сама идея инвестиций – вложения денег сейчас с целью получения дохо- да в будущем – основывается на идее прогнозирования будущего. Любая задача, связанная с манипулированием финансовыми инструментами, будь то валюта или ценные бумаги, сопря- жена с риском и требует тщательного расчета и прогнозирования

Поведение рыночного сообщества имеет много аналогий с поведением толпы, характе- ризующимся особыми законами массовой психологии. Частичная предсказуемость рынка обу- словлена относительно примитивным поведением игроков, которые образуют единую хаотиче- скую динамическую систему с небольшим числом внутренних степеней свободы.

Для успешной торговли на фондовом рынке необходимо выработать систему игры, ап- робированную на прошлом поведении временного ряда, и четко следовать этой системе, не поддаваясь влиянию эмоций.

Как известно, существуют два основных подхода к анализу рынка: технический и фунда- ментальный. Первый из них базируется на теории Доу, в основе которой лежит аксиома: «Цены учитывают все», и соответственно технический аналитик использует только цены актива и раз- личные индикаторы (функции цен). Фундаментальный анализ, наоборот, ищет взаимосвязь цен актива, внешних событий и данных типа макроэкономических показателей и финансовой отчет- ности корпораций и т.д.

Применение нейронных сетей в качестве дополнения дает уникальную возможность объ- единить эти два метода. Такой анализ, в отличие от технического, не имеет никаких ограниче- ний по характеру входной информации. Это могут быть как индикаторы данного временного ряда, так и сведения о поведении других рыночных инструментов, и внешние события. Нейро- сети активно используют на Западе институциональные инвесторы (например пенсионные фонды и страховые компании), работающие с большими портфелями, для которых особенно важны корреляции между различными рынками [1].

В отличие от технического анализа, основанного на общих рекомендациях и опыте трей- дера, нейросети способны строить оптимальную модель прогнозирования, более того, модель адаптивна и меняется вместе с рынком, что особенно важно для современных высокодинамич- ных финансовых рынков, в частности российского.

Применение нейронных сетей в финансах базируется на одном фундаментальном допу- щении – замене прогнозирования распознаванием. Нейросеть не предсказывает будущее, она «старается узнать» в текущем состоянии рынка ранее встречавшуюся ситуацию и максимально точно воспроизвести реакцию рынка.

Для прогнозирования финансовых временных рядов возможно использование много- слойных персептронов. Использование сетей с обратными связями в данном случае нецелесообразно в связи с трудностью обучения таких сетей и неактуальностью основной характеристики сетей с обратными связями – краткосрочной памяти.

Необходимо определить, какие входы подавать сети и какие данные получать на выходе. В общем случае входы сети отражают динамику торгов (цены и объемы) по исследуемому ин- струменту за некоторый предыдущий период времени. Выходом сети обычно выбирается изме- нение цены исследуемого финансового инструмента в будущем. Такой выход позволяет игроку принимать решения о совершении сделок на рынке.

Формирование входов нейронной сети

Несмотря на то что предсказания являются экстраполяцией данных, нейросети на самом деле решают задачу интерполяции, что существенно повышает надежность решения. Предска- зание временного ряда сводится к типовой задаче нейроанализа – аппроксимации функций многих переменных по заданному набору примеров с помощью процедуры погружения ряда в многомерное пространство.

Для динамических систем доказана следующая теорема Такенса. Если временной ряд порождается динамической системой, то есть значения t ? есть произвольные функции со- стояния системы, то существует такая глубина погружения d (примерно равная эффективному числу степеней свободы данной динамической системы), которая обеспечивает однозначное предсказание следующего значения временного ряда. Таким образом, выбрав достаточно большое d , можно гарантировать однозначную зависимость будущего значения ряда от его d предыдущих значений:

Хотя предсказание финансовых рядов сводится к задаче аппроксимации многомерной функции, оно имеет свои особенности как при формировании входов, так и при выборе выходов нейросети. Достаточно важным также является вопрос оценки качества финансовых предска- заний для выбора и построения наилучшей стратегии обучения нейросети.

В качестве входов и выходов нейросети не следует выбирать сами значения котировок (обозначим их t C ). Действительно значимыми для предсказаний являются изменения котиро- вок. Так как эти изменения обычно гораздо меньше по амплитуде, чем сами котировки, между последовательными значениями курсов имеется большая корреляция – наиболее вероятное значение курса в следующий момент равно его предыдущему значению:

Для повышения качества обучения следует стремиться к статистической независимости входов, то есть к отсутствию подобных корреляций. Поэтому в качестве входных переменных логично выбирать наиболее статистически независимые величины, например изменения коти- ровок t ?C или логарифм относительного приращения:

Использование логарифма относительного приращения является удачным для длитель- ных временных рядов, когда уже заметно влияние инфляции. В этом случае простые разности в разных частях ряда будут иметь различную амплитуду, так как фактически измеряются в раз- личных единицах. Напротив, отношения последовательных котировок не зависят от единиц измерения и будут одного масштаба несмотря на инфляционное изменение единиц измерения. В итоге большая стационарность ряда позволит использовать для обучения большую историю и обеспечит лучшее обучение.

Отрицательной чертой погружения в лаговое пространство является ограниченный «кру- гозор» сети, тогда как технический анализ не фиксирует окно в прошлом и использует доста- точно далекие значения ряда. Например, утверждается, что максимальные и минимальные значения ряда даже в относительно далеком прошлом оказывают достаточно сильное воздействие на психологию игроков и, следовательно, должны быть значимыми для предсказаний. Недостаточно широкое окно погружения в лаговое пространство не способно предоставить такую информацию, что, естественно, снижает эффективность предсказания. С другой стороны, расширение окна до таких значений, когда захватываются далекие экстремальные значения ряда, повышает размерность сети, что в свою очередь приводит к понижению точности нейросетевого предсказания уже из-за разрастания размера сети [2].

Альтернативный способ кодирования прошлого поведения ряда позволяет решить эту проблему. Интуитивно понятно, что чем дальше в прошлое уходит история ряда, тем меньше деталей его поведения влияет на результат предсказаний. Это обосновано психологией субъ- ективного восприятия прошлого участниками торгов, которые собственно и формируют буду- щее. Следовательно, представление динамики ряда должно иметь избирательную точность – чем дальше в прошлое, тем меньше деталей – при сохранении общего вида кривой

Одним из альтернативных способов кодирования временного ряда является использо- вание в качестве входных данных значений индикаторов технического анализа на относительно далеком периоде времени и значений колебаний курса в текущем периоде.

Также достаточно перспективным инструментом здесь может оказаться вейвлетное раз- ложение (wavelet decomposition). Оно эквивалентно по информативности лаговому погружению, но легче допускает такое сжатие информации, которое описывает прошлое с избирательной точностью.

Обучение нейронной сети

При обучении нейросетей, предназначенных для прогнозирования финансовых времен- ных рядов, используют стандартный подход. Имеющиеся примеры разбивают на три выборки: обучающую, валидационную и тестовую. Обучающая выборка предназначена для подстройки синаптических коэффициентов обучаемых нейронных сетей с целью минимизации ошибки на выходе сети. Валидационная выборка используется для выбора наилучших из нескольких обу- ченных сетей и/или для определения момента останова обучения. Тестовая выборка, которая не использовалась в процессе обучения, служит для контроля качества прогнозирования

Выбор функции ошибки

Для обучения нейросети недостаточно сформировать обучающие наборы входов- выходов. Необходимо также определить ошибку предсказаний сети. Среднеквадратичная ошибка не имеет большого «финансового смысла» для рыночных рядов. Например, для выбо- ра рыночной позиции надежное определение знака курса боле важно, чем понижение средне- квадратичного отклонения. Хотя эти показатели и связаны между собой, сети, оптимизирован- ные по одному из них, будут давать худшие предсказания другого.

Ошибка сети представляется в виде функции от синаптических коэффициентов и мини- мизируется одним из градиентных методов. Традиционно используют среднеквадратичную ошибку (суммирование производится по всем выходам):

Целью прогнозирования финансовых рядов является получение и максимизация прибы- ли. Поэтому в прогнозировании финансовых рядов важна не близость прогноза к истинному значению (что обеспечивает минимизация функции среднеквадратичной ошибки), а одинаковая направленность прогноза и истинного значения. Таким свойством обладает функция

Использование комитета нейросетей

Использование различных архитектур сетей, случайность выбора первоначальных синап- тических коэффициентов, а также использование других отличающих сети параметров – все это приводит к тому, что предсказания различных нейронных сетей, обученных на одних и тех же примерах, разнятся, иногда достаточно сильно. Явно «неудачные» варианты сетей отпада- ют на этапе валидации и тестирования. А более или менее «удачные» сети можно использо- вать совместно, организовав так называемый комитет сетей, используя для принятия реше- ния значения выходов всех входящих в комитет сетей [2].

Легко показать, что среднее значение выходов комитета должно давать лучшие предска- зания, чем средняя сеть из этого комитета. Это следует из неравенства Коши

Таким образом, предпочтительно использовать для принятия решения среднее значение выходов комитета нейросетей. Более того, можно использовать не среднее значение выходов, а среднее взвешенное. Веса выбираются адаптивно, максимизируя эффективность предсказа- ний комитета на обучающей выборке. В итоге лучшие сети будут вносить наибольший вклад, в то время как предсказания сетей, дающих худшие результаты, будут вносить меньший вклад и не будут портить предсказания.

Заключение

Использование нейронных сетей для анализа финансовой информации является пер- спективной альтернативой (или дополнением) для традиционных методов исследования. В си- лу своей адаптивности одни и те же нейронные сети могут использоваться для анализа не- скольких инструментов и рынков, в то время как найденные игроком для конкретного инстру- мента закономерности с помощью методов технического анализа могут работать хуже или не работать вообще для других инструментов.

Специфика объекта исследования накладывает некоторые особенности на использова- ние нейронных сетей для анализа данных. Такой особенностью является выбор функции ошиб- ки нейронной сети, отличной от традиционной среднеквадратичной. Следует отметить, что од- ной из важных составляющих анализа данных с помощью нейронных сетей является предоб- работка данных, направленная на сокращение размерности входов сети, повышение совме- стной энтропии входных переменных и нормировку входных и выходных данных.

Дальнейшая работа (авторов) в этой области будет направлена на эмпирические иссле- дования, такие как практическая реализация нейронных сетей и построение торговых систем на базе нейронных сетей.

Источник

Прогнозирование временных рядов нейронными сетями. Keras. Часть 1.

Продолжу рассматривать использование библиотеки Keras в решении задач различного рода. На этот раз рассмотрю, как работает прогнозирование временных рядов.

Разбираю код Дмитрия Романова, ведущего курс по нейронным сетям в «Университете Искуственного Интеллекта». Мой notebook с моделированием. Я немного оптимизировал код Дмитрия и добавил ряд пояснений, позволяющих разобраться в теме.

С временными рядами мы сталкиваемся повседневно. Это может быть описание каких-то природных событий, например, прогноз температуры, который жестко привязан к времени. Поменять местами последовательность нельзя, временной ряд рассыплется, если прогноз на 10-е поставить на 5-е число. Это будут совершенно другие данные. Т.е. делать перемешивание, как в случае, например, с определением авторства текстов, нельзя. К таким данным условно можно отнести многие, даже не представляющие собой зависимость именно от времени. Важно, что отсчеты нельзя менять местами. Например, аудиопоток, цены на акции, даже слова, поскольку изменить порядок букв в слове нельзя без искажения слова.

Обучающая выборка

Рассмотрим простой пример. Например, есть вектор, описывающий среднюю дневную температуру в течение 100 лет. Нужно построить прогноз на день вперед. Подготовим исходные данные для обучения сети.

Подготовка данных для анализа временных рядов на нейронных сетях

• xTrainCount = 36500 отсчетов — длина вектора описывающего погоду за 100 лет * 365 дней.
• xLen = 100 — длина вектора xTrain.
• stepsForward = 1 — длина вектора yTrain или количество шагов (дней) на которое делается прогноз погоды.
• Shft = 1 — смещение вектора xLen относительно предыдущего. Обычно смещение делают на единицу.
• xCount = xTrainCount — xLen + 1 – stepsForward — количество строк в матрице, которое получится после «раскусывания» исходного временного ряда на xLen + stepsForward.
• Выборка xTrain — матрица с размерностью (xTrainCount — xLen + 1 – stepsForward, xLen).
• Выборка yTrain — матрица с размерностью (xTrainCount — xLen + 1 – stepsForward, stepsForward).
• Каждое значение yTrain — это значение температуры в некоторый день, но оно определяется температурой за предыдущие xLen дней. Нейронка пытается обобщить, как значение yTrain длиной stepsForward (предсказание на 1 или более дней) зависит от значений xTrain длиной xLen. Т.е. в какой-то степени yTrain = f(xTrain).
• При таком перемешивании мы как бы ставим задачу нейронной сети найти взаимосвязь последовательности длиной stepsForward (например, в случае прогноза погоды на 1 день) из значений в исходной выборке от предыдущих xLen значений (например, от 50 предыдущих дней).
• Если мы задаем поиск закономерностей между значением yTrain длиной stepsForward и остальными значениями, то в случае, когда stepsForward > 1, мы тренируем нейронную сеть на предсказание на несколько дней вперед.
• При наличии нейронной сети, предсказывающей на 1 день вперед, можно сделать предсказание на 2 и более дней, подавая на вход значение, предсказанное нейронной сетью ранее и убирая с начала по одному дню, чтобы длина вектора не изменилась. Однако, для такого варианта точность предсказания нейронкой на один день должна быть очень высокой, иначе прогноз быстро станет случайным.

Проверочная выборка

Важный вопрос, как формируется проверочная выборка. В случае с временными рядами все не так просто, как с некоторыми другими данными. В данном случае нельзя случайным образом выбрать, например, 20% данных из xTrain и yTrain.
P.S. Цифры на графике обозначают некоторую общность данных — это не данные выборок. Например, желтые — это вектора относящиеся к xTrain.

• Проверочная выборка берется из векторов xTrain и yTrain.
• Для проверочной выборки берется «хвост» данных длиной valLen.
• Данные для проверочной выборки берутся снизу (с конца), чтобы быть максимально близкими к прогнозным значениям. Скажем, в случае прогноза погоды если взять начало последовательности, то это будут данные столетней давности. За 100 лет ситуация с погодой могла измениться, поэтому использовать их для проверки неправильно.
• Между проверочной выборкой и обучающей нужно сделать промежуток длиной xLen + stepsForward. В этом промежутке данные xTrain и xVal в значительной степени пересекаются. Нейронка может «заучить» на обучающей выборке общие с проверочной выборкой паттерны. Это может обманчиво улучшить показатели на проверочной выборке. Поэтому приходится пожертвовать данными из этого промежутка — они исключаются из выборок.
• При коротких выборках, когда данных мало, можно исключать не диапазон xLen + stepsForward , а меньше, например, 80% от этой длины или менее. Это уже в значительной степени уменьшает взаимное перемешивание.

Прогнозирование акций Лукойл

В предыдущей статье по нейронным сетям я уже рассмотрел загрузку данных с ftp/http. В данном случае URL для загрузки данных:

Загрузим данные из .csv с помощью Pandas. Нужно обратить внимание, что в качестве разделителя в csv используется «;» и в явном виде передать sep=’;’.

Что такое OHLC?

Видно, что показатели OHLC берутся с интервалом в 1 минуту.

OHLC – это сокращенное обозначение котировок, которые указываются для элементарной диаграммы ценового графика. В этой аббревиатуре :

• О обозначает Open – цену открытия интервала.
• H означает High (в нашем случае Max) — максимум цены интервала.
• L означает Low (Min) – минимум цены интервала.
• C означает Close – цену закрытия интервала.
• Volume — объем операций.

График OHLC

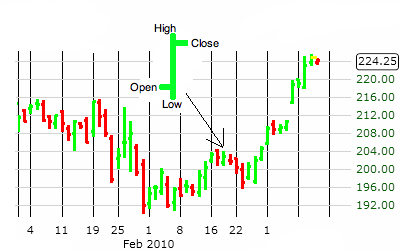
На графике OHLC каждый интервал времени (например, 5 минут) представлен OHLC ценами внутри этого интервала. OHLC — это один из основных показателей фьючерсной торговли на FOREX.

Подготовка данных

Для построения прогноза в данном случае не нужны колонки со временем и датой. Главное чтобы отсчеты брались через равные промежутки времени.

Файлы с данными по акциям идут по годам. Объединим два года для анализа.

Выведем данные OHLC на график:

Значения OHLC достаточно близки друг к другу, поэтому слились на первом графике.

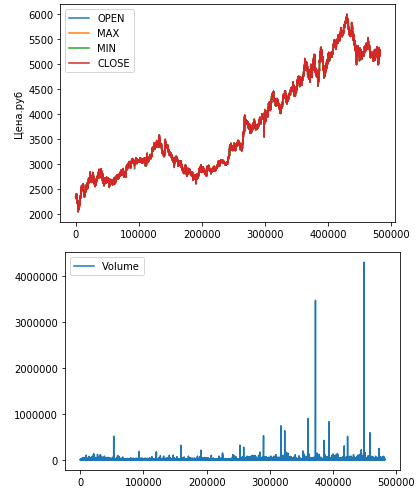
На втором графике видны два аномально высоких значения операций.

Проверка алгоритма подготовки данных

Смоделируем работу алгоритма по «раскусыванию» временного ряда на составляющие. Сгененирую простую последовательность, чтобы удобно ориентироваться в работе кода:

Исходную последователность преобразуем в массив «раскусыванием»:

Для получения yTrain нужно в каждой строке брать вектор длиной stepsForward, начиная с xLen, поскольку последовательность до xLen пошла в xTrain. Соотвественно, range начнется с xLen.

Видно, что значения вектора yTrain начинаются с xLen. Каждый элемент длиной stepsForward = 1. По сути, нейронка ищет закономерность между каждым yTrain и предыдущими xLen значений xTrain.

После получения исходной последовательности нужно разрезать массив на две части: обучающую выборку и валидационную. Кроме того между ними нужно выбросить «прослойку» размером bias записей. Это важно, чтобы гарантированно исключить перемешивание, т.е. чтобы в валидационную выборку не попали значения из обучающей.

В следюущей статье я сделал другой вариант разбивки на обучающую и проверочную выборку, он компактнее и понятнее.

После запуска «раскусывалки» получим следующее:

• 3 записи остались для для проверочной выборки.
• 8 записей были выброшены (bias)
• 4 записи с начала оставлись для обучающей выборки

итого 15 записей.

Код подготовки данных для временного ряда

Одномерная свертка

Забегая вперед скажу, что на этом временном ряде наилучшие показатели обеспечила одномерная свертка.

Источник