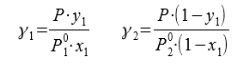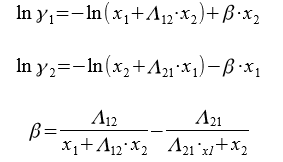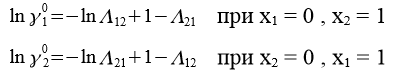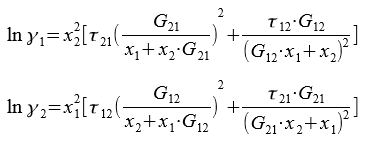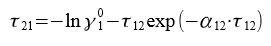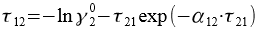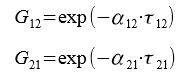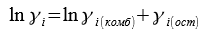Полуэмпирическая модель предсказания коэффициентов активности называется unifac

Моделирование коэффициентов активности компонентов системы ацетон — пропанол с помощью уравнений Вильсона, NRTL и UNIFAC

Дата публикации: 21.03.2020 2020-03-21

Статья просмотрена: 200 раз

Библиографическое описание:

Остапчук, А. В. Моделирование коэффициентов активности компонентов системы ацетон — пропанол с помощью уравнений Вильсона, NRTL и UNIFAC / А. В. Остапчук. — Текст : непосредственный // Молодой ученый. — 2020. — № 12 (302). — С. 1-7. — URL: https://moluch.ru/archive/302/68216/ (дата обращения: 07.07.2021).

В данной работе описываются способы определения коэффициентов активности изотермической системы ацетон — пропанол с помощью полуэмпирических методов расчёта и с помощью модели UNIFAC.

Физико-химические свойства системы

Основные физико-химические параметры компонентов системы

Ацетон

Пропанол

Температура плавления, °C

Температура кипения, °C

Молярная масса, г/моль

Ацетон — бесцветная подвижная летучая жидкость с характерным резким запахом. Во всех соотношениях смешивается с водой, диэтиловым эфиром, бензолом, метанолом, этанолом, многими сложными эфирами. Органическое вещество, имеющее формулу CH3–C(O)–CH3, простейший представитель насыщенных кетонов.

Пропанол — одноатомный спирт. Встречается в природе в небольших количествах как продукт ферментации. Бесцветная жидкость со спиртовым запахом, смешивается с водой и образует с ней азеотропную смесь. Растворим в этаноле, диэтиловом эфире, ацетоне, бензоле и других органических растворителях.

1) Бинарная система (ацетон — пропанол)

2) Паровая фаза считается идеальной (подчиняется закону Дальтона)

3) Давления насыщенных паров компонентов системы рассчитаны по уравнению Антуана

4) Коэффициенты активности компонентов системы рассчитаны по методу UNIFAC

5) Система изотермическая (25 0 С)

Подставив исходные данные в программу ChemSep, были получены данные о равновесии в системе:

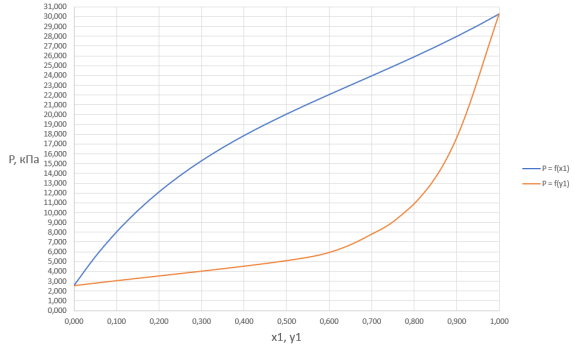
Рис. 1. График зависимости общего давления в системе от содержания ацетона в жидкой и газовой фазах

Составы равновесных фаз для системы ацетон (1) –пропанол (2) при общем давлении Ри температуре 25º C

Температура, 0 С

доля C3H6O

в жидкой фазе

доля C3H6O

в паровой фазе

Общее

давление, кПа

Давление чистого

C3H6O, кПа

Давление чистого

C3H7OH, кПа

В связи с низким общим давлением в системе при заданной температуре и отсутствием сильной ассоциации компонентов в паровой фазе считаем данную паровую систему идеальной. При этом допущении расчет коэффициентов активности компонентов возможен по уравнению:

Где х₁, у₁ — доли ацетона в жидкой и паровой фазах соответственно

Р — общее давление в системе

,− давление чистых ацетона и пропанола соответственно

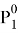
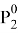
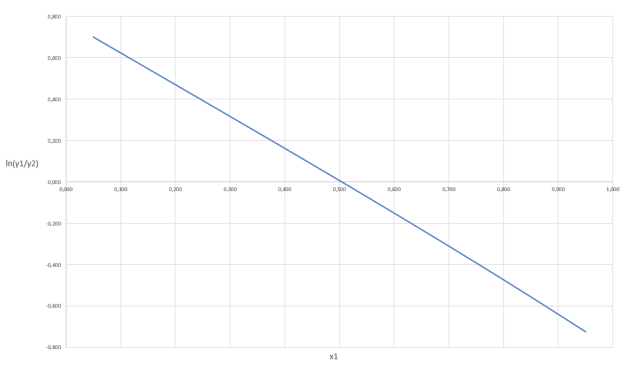
Построив график зависимости ln(γ₁/γ₂) = f(x₁) можем сделать вывод о термодинамической согласованности данных.

Рис. 2. График зависимости логарифма отношения коэффициентов активности от содержания ацетона в жидкой фазе

Так как площадь под графиком равна 0, то система является термодинамически согласованной.

Полуэмпирические модели

В случае полуэмпирических моделей структура модельных уравнений выводится из теории растворов, но обработка экспериментальных данных совершается с использованием регрессионных параметров.

Модель Вильсона

Наибольшее распространение обрела модель «локальных составов». Первое уравнение, образованное на этой модели, было выведено в 1964 г. Вильсоном. Модель «локальных составов» основана на том, что в результате межмолекулярных взаимодействий в смеси начинаются локальные микросоставы, неэквивалентные макросоставу раствора по приготовлению. Разница локальных и средних концентраций компонентов связанна с разностью энергией взаимодействия одноименных и разноименных пар молекул.

Для расчета коэффициентов активности компонентов бинарной системы применяются следующие уравнения:

Где Λ₁₂, Λ₂₁ — приведенные параметры, оцениваемые по экспериментальным данным для данной системы.

Между параметрами уравнения Вильсона и коэффициентами активности компонентов при бесконечном разбавлении получаются следующие зависимости:

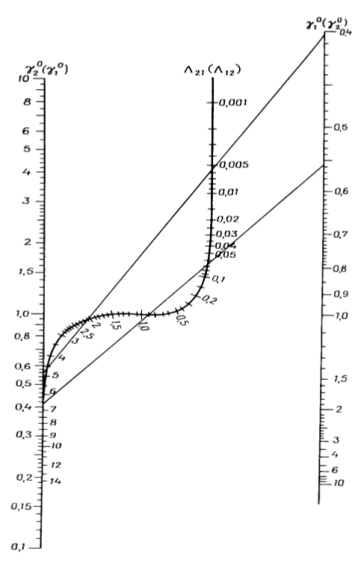
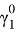
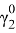
С помощью номограммы определяем начальные значения Λ₁₂ = 0,7, Λ₂₁ = 0,6 при = 2,16, = 2,28 и рассчитываем уточненные значения приведенных параметров.

В итоге получаем вытекающие значения приведенных параметров: Λ₁₂ = 0,693, Λ₂₁ = 0,596. Далее ищем значения β и затем ɣ₁, ɣ₂.

Главный минус модели Вильсона заключается в том, что уравнение, как правило хорошо описывающее равновесие жидкость — пар, непригодно для представления данных о равновесии жидкость — жидкость.

Значительное преимущество уравнения Вильсона в сравнении с эмпирическими уравнениями — способность описания поведения многокомпонентных смесей, если известны приведенные параметры для всех составляющих бинарных систем.

Предложены различные модификации уравнения Вильсона, разрешающие ликвидировать его главный недостаток — плохое описание поведения гетерогенных систем.

Рис. 3. Номограмма для определения приведенных параметров уравнения Вильсона

Модель NRTL

Одна из модификаций была выведена Реноном и Прауснитцем в 1968 г. уравнение NRTL (nonrandom two-liquid). Оно также основано на концепции локальных составов и на теории, согласно которой жидкость имеет ячеистую структуру.

Для бинарной системы:

Приведённые энергетические параметры τ₁₂ и τ₂₁ находим, решив систему уравнений:

Далее находим переменные G₁₂ и G₂₁, характеризующие энергию взаимодействия:

α₁₂ = 0,5 — параметр, характеризующий степень упорядоченности распределения молекул в растворе

Решая системы уравнений, находим значение переменных τ₁₂ = 0,515 и τ₂₁ = 0,372. Далее находим G₁₂ = 0,773 и G₂₁ = 0,83.

Математическая форма уравнений обеспечивает модели NRTL большую гибкость, способность описывать самые различные типы зависимости коэффициентов активности от состава. Сохраняя основные достоинства уравнений Вильсона, уравнения NRTL способны также описывать системы с расслаиванием, благодаря чему их часто используют для расчета равновесий жидкость — жидкость и жидкость — жидкость — пар.

Теоретические модели. Метод UNIFAC

Теоретические модели позволяют рассчитывать коэффициенты активности на основании свойств чистых компонентов.

Метод UNIFAC (universal functional activity coefficient — универсальный функциональный коэффициент активности) был разработан в 1975 году Фреденслундом, Джонсом и Праузницем. Данный метод рассчитывает величины коэффициентов активности на основе концепции группового вклада. Предполагается, что взаимодействия между двумя молекулами являются функцией взаимодействий между группами. Для расчета коэффициентов активности этим групповым методом применяется вариант модели локальных составов UNIQUAC. Уравнение UNIQUAC (UNIversal QUAsi-Chemical equation), совмещает в себе концепцию локального состава с квазихимической решеточной теорией Гуггенгейма — Ставермана. Величины коэффициентов активности γ_i рассматривают как сумму двух вкладов — комбинаторного, обусловленного различиями в размерах и форме молекул, и остаточного, определяемого в основном энергетикой межмолекулярных взаимодействий.

Для расчета коэффициентов активности компонентов бинарной системы при заданной температуре и составе системы молекулы компонентов разбиваются на подгруппы.

Геометрические параметры модели UNIFAC

№группы

По UNIFAC

Группа

R_k

Q_k

Количество групп вмолекуле

Источник

Теоретические основы математического моделирования химико-технологических процессов и систем управления

Обзор типовых математических моделей химико-технологических процессов

1. Блочный принцип построения математических моделей химико-технологических процессов (ММ ХТП)

Математическая модель ХТП в общем случае включает в себя следующие математические описания «элементарных» стадий процесса:

1. движение потоков фаз;
2. химические превращения;
3. массо- и теплоперенос в потоках фаз;
4. массо- и теплопередача между потоками фаз;
5. изменение агрегатного состояния фаз.

Блочный принцип построения математической модели ХТП заключается в выборе элементарных стадий процессов, каждый из которых исследуется отдельно. Далее ММ элементарных стадий объединяются в результирующую модель.

Этапы построения ММ ХТП

1) Исследуют гидродинамическую структуру ХТП – основу будущей модели. Эта часть отражает поведение ХТП без учета физико-химических превращений, но с реальными нагрузками на объект по фазам.

2) Изучают кинетику химических реакций, скорости процессов массо- и теплопередачи, кинетику фазовых переходов и составляют соответствующие элементарные функциональные зависимости, которые дополняются начальными и граничными условиями и различного рода ограничениями.

3) Объединяют модели элементарных процессов в общую результирующую математическую модель ХТП.

Состав ММ ХТП в общем случае имеет вид:

Структура уравнений математических моделей химико-технологических процессов основана на балансовых соотношениях сохранения массы, энергии, импульса с учетом гидродинамической структуры потока и показана на следующем рисунке.

Источник

Модель UNIFAC 48

4.8.1. Модель UNIFAC 48

Метод UNIFAC (universal functional activity coefficient – универсальный функциональный коэффициент активности) был разработан в 1975 году Фреденслундом, Джонсом и Праузницем. Данный метод рассчитывает величины коэффициентов активности на основе концепции группового вклада. Предполагается, что взаимодействия между двумя молекулами являются функцией взаимодействий между группами. Данные межгруппового взаимодействия получаются путем обработки экспериментальных данных для пар компонентов. Число функциональных групп ограничено.

Метод UNIFAC основан на модели UNIQUAC, которая представляет избыточную энергию Гиббса (и логарифм коэффициента активности) как комбинацию двух эффектов. Таким образом, используется уравнение:

(4.8.1.)

Комбинационный член рассчитывается непосредственно по уравнению UNIQUAC с использованием параметров площади и объема Ван дер Ваальса, рассчитанных по индивидуальным структурным группам :

(4.8.2.)

(4.8.3.)

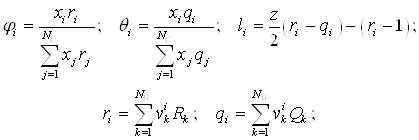
N_C – число компонентов;

N_G – число различных групп в смеси;

z – согласованное число для пространственной решетки, равное 10;

– число функциональных групп типа k в молекуле i;

R_k – параметр объема для функциональной группы k;

Q_k – параметр площади для функциональной группы k;

x_i – мольная доля компонента i в жидкой фазе.

Параметры группового объема и площади определяются из атомной и молекулярной структуры:

(4.8.4.)

где : V_k, A_k = объем и площадь Ван дер Ваальса для группы k;

Остаточный член определяется как:

(4.8.5.)

где: Г_k = остаточный коэффициент активности группы k в смеси;

= остаточный коэффициент активности группы k в стандартном растворе, содержащем только молекулы, состоящие из групп типа i.

Остаточный коэффициент активности определяется выражением:

(4.8.6.)

где : m, n = 1, 2, . N_G.

Параметр τ_mn определяется как

(4.8.7.)

где : a_mn – параметр бинарного взаимодействия для групп m и n.

Принимается, что параметр бинарного взаимодействия a_mn постоянен и не зависит от температуры.

5. Постановка задачи

Целью данной работы являлась структурная и параметрическая оптимизация технологической схемы разделения смеси бензол-хлорбензол-дихлорбензол для снижения энергозатрат на разделение.

Для достижения поставленной цели необходимо:

• выбрать математическую модель парожидкостного равновесия, адекватно описывающую экспериментальные данные;

• синтезировать схемы разделения;

• произвести расчет ректификации и выбрать решение, обеспечивающее минимальные энергозатраты.

6. Расчетная часть.

6.1. Методы и алгоритмы исследования

В настоящей работе для математического моделирования схем ректификации использован лицензионный программный комплекс PRO/II with PROVISION компании SIMSCI corp., обеспечивающий моделирование и расчет технологических схем ректификации.

PRO/II — компьютерный комплекс для инженерных расчетов процессов органического синтеза и нефтехимии, технологии полимеров и др. Он объединяет базы данных химических компонентов и расширенных методов расчета термодинамических свойств с гибкими методами расчета аппаратов. Программа обладает вычислительными средствами для выполнения расчетов всех материальных и энергетических балансов необходимых для моделирования большинства статических процессов. Экспертные системы, расширенная обработка входных данных и проверка ошибок обеспечивают его высокую эффективность и надежность.

6.2. Расчет ректификации

Все алгоритмы ректификации в программе PRO/П представляют собой строгие модели равновесных ступеней контакта. В каждой модели решаются тепловой и материальный балансы и уравнения равновесия жидкость — пар.

Программа PRO/II предлагает четыре различных алгоритма моделирования ректификационных колонн:

алгоритм Inside/Out (I/O),

алгоритм Chemdist и

Алгоритм I/O может быть использован для решения большинства задач нефтепереработки и обладает высоким быстродействием. В настоящей работе расчет колонн ректификации проводился по этому алгоритму.

Алгоритм подразделяется на внешний и внутренний циклы. Во внутреннем цикле решаются тепловой и материальный балансы и обеспечиваются заданные требования. Во внутреннем цикле используются методы, основанные на расчете коэффициентов активности на основе концепции группового вклада.На рис. 6.2.1. показана схематическая диаграмма простой ступени контакта.

Рис. 6.2.1.. Схема простой ступени контакта алгоритма I/O.

Тепловой баланс для ступени контакта j выглядит следующим образом:

где: V— расход пара, покидающего ступень контакта;

где: V— расход пара, покидающего ступень контакта;

L — расход жидкости, покидающей ступень контакта;

Ls — жидкостной боковой погон;

V_s — паровой боковой погон;

Материальный баланс по компоненту для данной ступени контакта через расходы жидкости и паров при следующей зависимости для равновесных составов обеих фаз:

где К представляет собой соотношение равновесной фугитивности пар — жидкость, может быть записан как:

где: — расход жидкого компонента;

v — расход парового компонента;

f- расход компонента сырья.

6.3. Объект исследования

В качестве побочных продуктов при синтезе хлорбензола получаются дихлорбензолы и трихлорбензолы. Общее содержание побочных продуктов в потоке приблизительно равно 1,5% масс. Так как в этой работе не ставилась задача получения всех побочных продуктов в качестве отдельных продуктовых потоков в рассматриваемой нами смеси все побочные продукты были заменены на самый легкокипящий из них – метадихлорбензол. Далее смесь продуктов синтеза хлорбензола будет рассматриваться как трёхкомпонентная зеотропная смесь: бензол — хлорбензол — метадихлорбензол. В качестве технических требований к готовым продуктам приняты требования по ГОСТ 646-73 для хлорбензола и по ОСТ 6-01-392-74 для дихлорбензола. Качество продуктов в мольных долях соответствующее стандартам приведено в таблице 6.3.1.

Составы потоков в мольных долях.

Компоненты	Поток питания	Бензол	Хлорбензол	Дихлорбензол
Бензол	0,7258	0,9965	0,0015	0,0
Хлорбензол	0,2652	0,0035	0,9985	0,026
Метадихлорбензол	0,009	0,0	0,0	0,974

Индивидуальные свойства компонентов представлены в таблице 6.3.2.

Физико-химические свойства чистых компонентов

Плотность, кг/м 3

Молекулярная масса, г/моль Бензол 80,09 883,92 78,11 Хлорбензол 131,68 387,0 112.56 М-Дихлорбензол 172,81 1288,1 147,004

Коэффициенты уравнения Антуана.

А В С Бензол 15,9008 2788,51 -52,36 Хлорбензол 16,0676 3295,12 -55,6 М-Дихлорбензол 16,8173 4104,12 -43,15

Самый легколетучий компонент в исследуемой смеси — бензол, который является родоначальником углеводородов ароматического ряда. Химические свойства пределяются наличием в молекуле стабильной замкнутой системы -электронов. Для бензола характерна устойчивость к действию высоких температур и окислителей. Лишь выше 650 0 С он частично превращается в дифенил, выше 750 0 С разлагается на углерод и водород

Основное области применения бензола ( более 80 %) – производство этилбензола, кумола, циклогексана. Остальное количество бензола –для получения анилина, малеинового ангидрида, как компонент моторного топлива для повышения октанового числа , как растворители и экстрагент в производстве лаков, красок ,ПАВ и др.

Хлорбензол- бесцветная жидкость с характерным запахом. Хорошо растворим в органических растворителях, растворимость в воде 0,049% по массе (30 0 С), образует азеотропную смесь с водой.

Дихлорбензол растворим а этаноле и диэтиловом эфире. П-дихлорбензол так же растворим в бензоле, хлороформе и хлоре. При хлорировании в присутствии FeCl₃ дихлорбензол превращается в 1,2,4-трихлорбензол (из орто-дихлорбензола образуется также небольшое количество 1,2,3-трихлорбензола).Дальнейшее хлорирование дает Петро-, пента и гексахлорбензолы

В промышленности о-дихлорбензол и п-дихлорбензол выделяют из смеси полихлоридов бензолов, образующихся как побочные продукты в производстве хлорбензола. После отгонки основного количества хлорбензола темную жидкость, содержащую 3-4 % хлорбензола 55-60 % п-дихлорбензола, 35-38 % о-дихлорбензола, примеси трихлорбензолов и смолообразных веществ; осветляют дистилляцией (130 0 С,20 кПа),подвергают кристаллизации(0-5 0 С) и центрифугированием отделяют п-дихлорбензол.

6.4. Выбор адекватной модели.

Систематическое исследование процессов ректификации требует выбора адекватной модели парожидкостного равновесия. В настоящей работе расчетный эксперимент поставлен на примере разделения многокомпонентной модельной смеси бензол — хлорбензол — метадихлорбензол.

Выбор модели описания парожидкостного взаимодействия для смесей бензол-хлорбензол производился на основании сопоставления экспериментальных и расчетных данных. Расчет парожидкостного равновесия проведен с использованием программного комплекса PRO/IL и её базы данных. На основании имеющегося опыта практического использования и общих рекомендаций по применению выбрано несколько моделей ПЖР, реализованных в программном комплексе:

I — NRTL, II — модель SRK, III – Wilson, IV – UNIQUAC, V – UNIFAC.

В качестве критерия сравнения для статистической обработки результатов было выбрано среднее относительное отклонение описания паровой фазы, δ.

где N- количество экспериментальных точек фазового равновесия.

Экспериментальные данные по парожидкостному равновесию пары бензол – хлорбензол.

X мол.дол.	Y мол.дол.	t, °С	P, мм.рт.ст.
5.3	17.4	126.4	760
10.4	31.1	121.8
19.2	48.0	115.1
29.5	62.8	108.2
29.6	62.9	108.2
39.9	73.1	102.7
51.4	81.6	97.1
59.1	86.0	93.9
68.4	90.4	90.3
70.3	91.2	89.5
78.6	94.2	86.7
80.4	95.0	86.1
88.4	97.1	83.5

Результаты моделирования парожидкостного равновесия

Смесь	δ,%
	NRTL	UNIQUAC	Wilson	SRK	UNIFAC
Бензол — хлорбензол	2,21	0,665	0,649	1,48	0,627

Судя по среднему относительному отклонению от экспериментальных данных по парожидкостному равновесию, как видно в таблице 6.4.2., наиболее адекватно равновесие бинарной пары бензол-хлорбензол описывает модель UNIFAC. Данные для пар содержащих метадихлобензол в базе данных PROII есть только для модели UNIFAC, поэтому для дальнейших расчётов была принята модель UNIFAC.

6.5. Синтез схем ректификации для разделения смеси бензол-хлорбензол-м-дихлордензол

Для разделения трехкомпонентной зеотропной смеси нами было предложено четыре технологические схемы (рис. 6.5.1. — 6.5.2.). Две из них являются последовательностью из простых двухсекционных колонн, две другие — являются комплексами из сложных колонн с боковыми секциями. В ряде случаев применение сложных колонн оправдано за счет приближения к термодинамической обратимости за счет структурных особенностей. Кроме того, такие схемы требуют меньшее число кипятильников и дефлегматоров, что может привести к значительному снижению энергозатрат на разделение. Но следует помнить, что такие технологические схемы целесообразно применять при невысокой четкости разделения и содержании среднекипящего компонента более 20%.

Рассмотрим предложенные схемы более подробно.

Схема 1 представляет собой последовательность простых двухсекционных колонн, работающих в режиме первого заданного разделения (рис. 6.5.1.а, в). Согласно этой схеме в качестве дистиллата колонны 1 выделяют практически чистый бензол, а кубовый продукт колонны 1 поступает на дальнейшее разделение. В колонне 2 происходит разделение хлорбензола и метадихлорбензола.

Технологическая схема 2 представлена на рис. 6.5.2. а, в. Первая колонна схемы 2 работает в режиме второго заданного разделения, что позволяет выделить в качестве кубового продукта тяжелокипящий метадихлорбензол. Дистиллат колонны 1 направляют на дальнейшее разделение на бензол и хлорбензол в колонну 2.

Используя широко развитые методы синтеза схем, основанные на теории графов [5, 6, 7, 8], нами синтезированы технологические схемы разделения трехкомпонентной смеси бензол — хлорбензол – метадихлорбензол, содержащие сложные колонны (рис.6.5.1. б, г, 6.5.2. б, г). Схемами-прообразами являются описанные схемы 1 и 2. Для трансформации схем 1 и 2 представим их в виде графов (рис. 6.5.1. в, г, 6.5.2. в, г). Структуры 3 и 4 получают путем стягивания по ориентированному ребру, эксплицирующему потоки между колоннами. Полученные схемы-образы являются структурами с частично (рис. 6.5.1.б,г, 6.5.2.б,г) связанными тепловыми и материальными потоками.

Синтезированная схема 3 (рис. 6.5.1. б) представляет собой сложную колонну с боковой укрепляющей секцией. Схема содержит два дефлегматора и один кипятильник. Схема 4 (рис. 6.5.2. б), напротив, отличается наличием двух кипятильников и одного дефлегматора, представляя тем самым сложную колонну со стриппинг-секцией.

Таким образом, нами предложено четыре схемы разделения, представленные на рис.6.5.3.(схема1, схема2) и рис. 6.5.4. ( схема3, схема4).

Источник