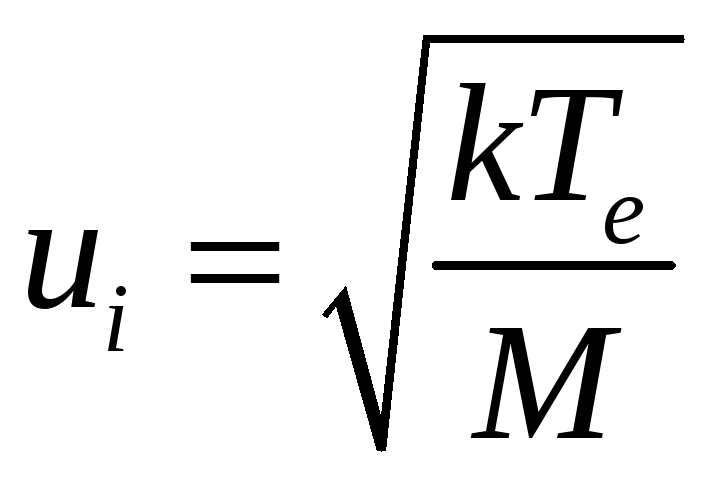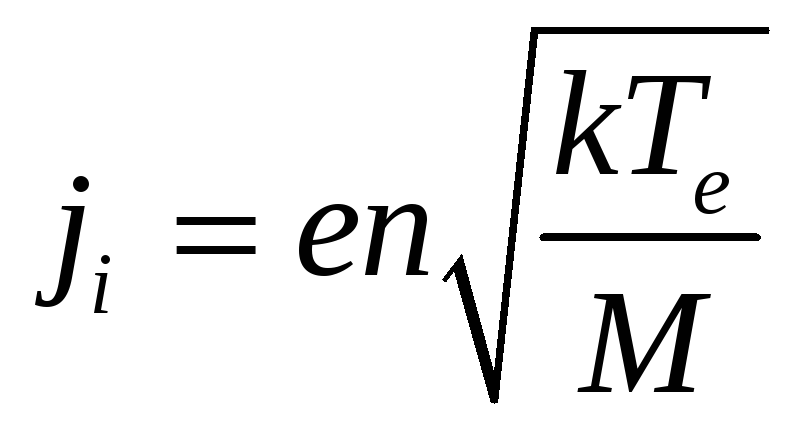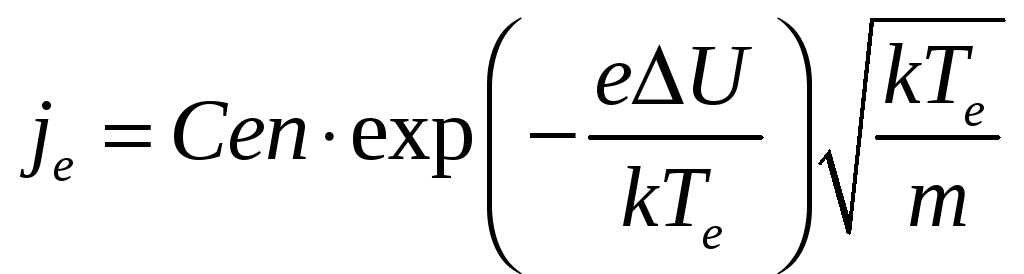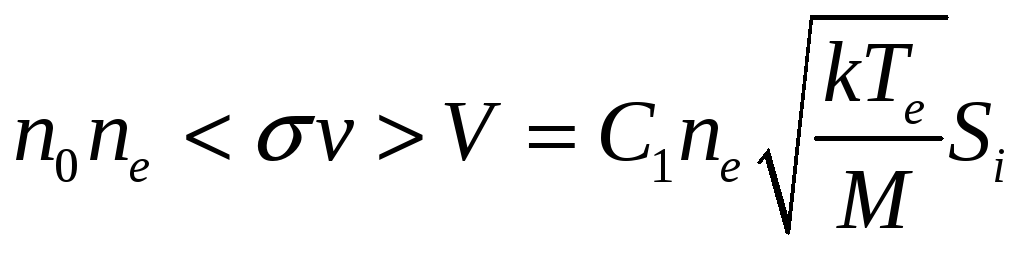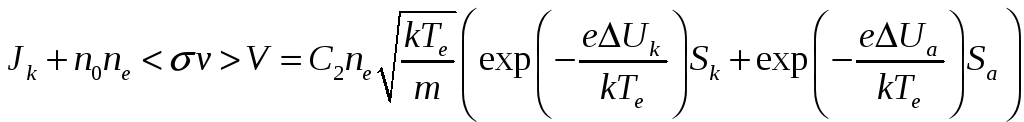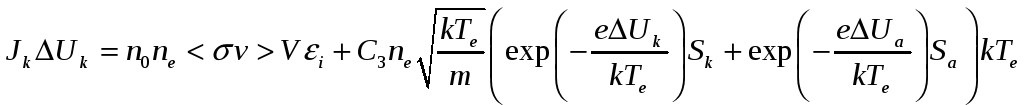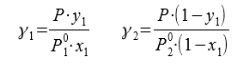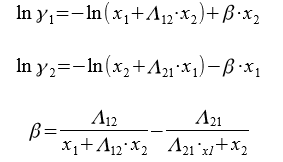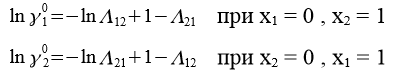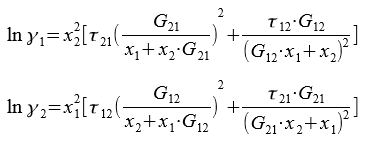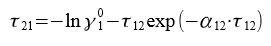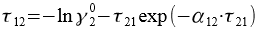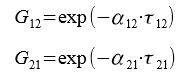Полуэмпирическая модель предсказания коэффициентов активности называется nrtl

Полуэмпирические модели

Выше упоминалось, что полуэмпирическими методами называются методы, в основе которых лежит какая-то простая математическая модель. Все, что не удается посчитать простыми средствами, при этом учитывается с помощью эмпирических поправок. Иногда в качестве математической модели в полуэмпирических методах используется аналитические решения для какой-то более простой задачи. При этом поправочные коэффициенты учитывают различия между реальной задачей и той, для которой построено аналитическое решение. К сожалению, аналитические решения крайне редки.

За этим нехитрым (хотя и нечетким) определением скрывается великое множество математических моделей. Но этому множеству, в некотором смысле, очень не повезло: те, кто пишут книги по математическому моделированию, предпочитают либо вообще не упоминать о полуэмпирических методах, либо ограничиться констатацией факта их существования. Никакой общепринятой классификации этих методов не существует. Здесь, естественно, никакой классификации предлагаться не будет, просто приведу несколько примеров, демонстрирующих применение полуэмпирических методов.

На самом деле эти методы настолько распространены, что многие специалисты даже не задумываются о том, что большинство инженерных методик, применяемых в конструкторских бюро, (по крайней мере, по формальным признакам) относятся к полуэмпирическим методам. Для начала рассмотрим две простейшие модели.

Как двигателист будет оценивать массу энергетической установки на базе солнечных батарей? Он возьмет мощность потребителей энергии и времена в течение которых солнечные батареи будут находится в тени и на освещенном участке орбиты. Оценит емкость аккумулятора, необходимую для питания нагрузки при нахождении аппарата в тени. По удельной массе аккумулятора оценит массу аккумуляторных батарей. Исходя из характерных времен оценит потребную мощность солнечных батарей. По их удельной массе оценит массу солнечных батарей и, наконец, массу установки в целом. При этом все используемые формулы «точные», но входящие в них коэффициенты (кпд аккумулятора и солнечных батарей, удельные массы аккумулятора и солнечных батарей) эмпирические.

Аналогично поступит специалист по энергетическим установкам, если ему потребуется оценить массу двигательной установки. Исходя из суммарного импульса, который должна отработать двигательная установка, ее удельного импульса и коэффициента использования рабочего тела оценивается масса рабочего тела. Через баковый коэффициент оценивается масса системы хранения и подачи рабочего тела. Через тягу можно оценить массу двигателя. Здесь тоже во всех формулах используются эмпирические коэффициенты.

Следует отметить, что использование эмпирических данных вовсе не означает, что аналогичные данные не могут быть получены расчетным путем. Например, кпд устройства, как правило, может быть рассчитан. Но, если точность эмпирических данных устраивает заказчика, то использование эмпирики просто экономит ресурсы (в первую очередь время).

А что делать, если точности не хватает? Как правило, вводятся дополнительные поправки. Например, в приведенных выше примерах можно учесть массу вспомогательного оборудования, резервирование и запасы (рабочего тела, мощности и т.п.). Можно уточнять существующие коэффициенты. Например, можно использовать более сложные формулы для расчета кпд или удельной массы, учитывающие какие-то параметры конструкции. Как показывает практика, при наличии достаточного количества экспериментальных данных, всегда можно построить сравнительно простую полуэмпирическую модель, позволяющую получать все основные характеристики разрабатываемой конструкции с требуемой точностью.

Упоминавшиеся выше полуэмпирические модели относятся к устройствам, использующим плазму. Теперь рассмотрим применение полуэмпирических моделей к описанию параметров самой плазмы. Если набраться наглости, то полуэмпирическими можно объявить закон Бома о сопротивлении плазмы в магнитном поле и закон Кулона. Я предпочитаю считать эти законы эмпирическими потому, что более или менее строгая теория под них была подведена после открытия этих законов.

По многичсленным просьбам учащихся привожу одну из формулировок закона Бома о сопротивлении плазмы в магнитном поле. Рассматривается задача прохождения потока электронов со скоростью u через участок поперечного магнитного поля. Ширина участка L, индукция магнитного поля B. Концентрация тяжелых частиц составляет n₀, рассеяние электронов на этих частицах определяется величиной , разность потенциалов на концах участка Δφ. Согласно классической теории (в предположении, что радиус Лармора электронов много меньше ширины участка) все перечисленные выше величины связаны соотношением:

Особое внимание в данной формуле следует обратить на вторую степень при индукции магнитного поля. На практике часто наблюдалась линейная зависимость от индукции магнитного поля. Посмотрев на такие экспериментальные данные Бом предложил другое соотношение, получившее теперь его имя:

Но другому достижению Бома – формуле для скорости ионов на границе плазма-пристеночный слой 5 – больше «повезло» на полу­эм­пи­ри­чес­кие применения. Итак, формула выглядит как

Еще одно лирическое отступление, отвечающее на вопрос: почему в формулу скорости ионов входит температура электронов? Привожу нестрогое, зато простое доказательство. Рассмотрим «окрестность границы плазма-слой». Индексом b будем обозначать значение на границе плазма-слой. В плазме концентрации ионов и электронов совпадают, поэтому никакого индекса им давать не буду. Итак, для ионов имеем

Выберем начало отсчета потенциала так, чтобы энергию ионов можно было записать формулой

Из нее получаем, что при незначительном изменении потенциала концентрация ионов описывается соотношением

n_i=n_b .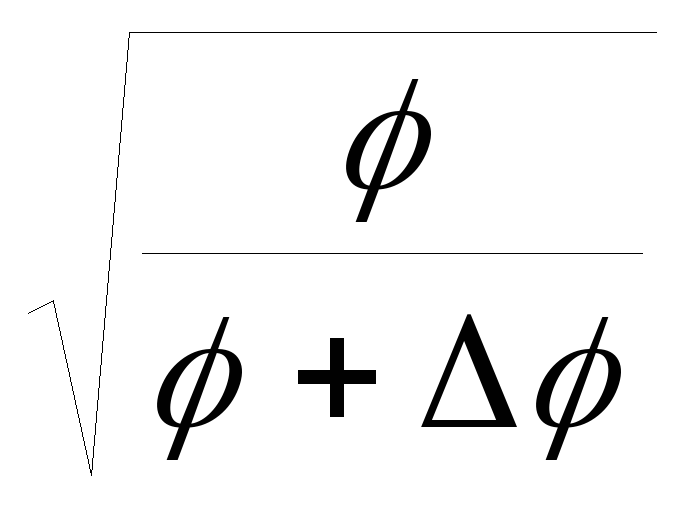

Считая изменения потенциала незначительными можно упростить формулы для концентраций

Уравнение Пуассона для электрического потенциала при этом можно записать в виде

Так как известно, что вторая производная потенциала отрицательна, получаем

φ>.

В силу нашего определения потенциала имеем

u_ib=.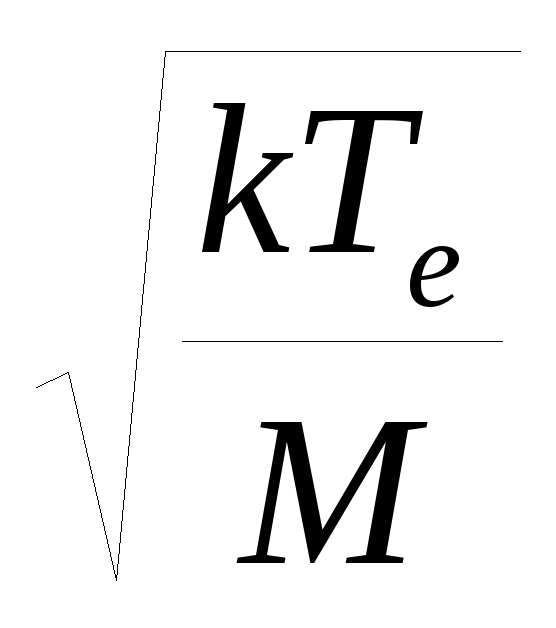

Согласно литературным источникам [6] изначально эта формула была выведена Тонксом и Ленгмюром, а затем приведенный здесь упрощенный вывод был сделан Бомом. Теперь эта формула носит его имя.

Из нее следует, что ионный ток на стенку составляет (в случае однозарядных ионов)

Формула точная, но определить концентрацию на границе плазма/пристеночный слой сложно. Гораздо проще определить концентрацию на некотором расстоянии от стенки, где влияние стенки заметно ослабевает. Но как связаны между собой эти концентрации? Для простейшего случая это можно найти аналитически (см. [6]). Но чаще вводят эмпирический коэффициент. В этот коэффициент может вставляться не только отношение концентраций, но и, например, отношение «эффективной» (собирающей) поверхности к реальной. Например, в книге [7] приводятся коэффициенты для зондов различной формы для различных диапазонов параметров плазмы. Аналогично поступают с электронным током. Для простейших случаев можно вывести аналитические формулы (см. например [6]). В общем случае можно записать полуэмпирическую формулу

где C – эмпирический коэффициент.

Другой характерный пример применения полуэмпирики – использование «эффективного потенциала ионизации с учетом радиационных потерь». Как просто рассчитывать процессы ионизации? Как известно далеко не каждый электрон при столкновении с нейтральной частицей ионизует ее, даже если его энергия больше потенциала ионизации. В большинстве случаев происходит лишь возбуждение. Наиболее честный способ расчета плазмы при этом – для каждого уровня возбуждения завести группу частиц и методично рассчитывать переходы из одной группы в другую. Но такой подход требует больших затрат ресурсов. Желание экономить привело к простому решению: считать только одну группу нейтральных частиц, ионизация которых происходит за одно столкновение, но на ионизацию требуется некоторая «эффективная энергия ионизации», зависящая от температуры электронов. Эта «эффективная энергия» учитывает радиационные потери, поэтому она выше энергии ионизации, приводимой в справочниках. Естественно, что при этом используется «эффективное сечение столкновения».

Рассмотрим теперь, как часто рассчитываются параметры плазмы в газоразрядных устройствах. Концентрации частиц считаются примерно одинаковыми в рассматриваемой области. Для каждой группы частиц составляются уравнения баланса: количество «родившихся» частиц приравнивается к количеству «уходящих». Дополнительно составляется баланс энергии. Для примера составим уравнения для некого абстрактного газоразрядного устройства. Будем считать концентрацию нейтральных частиц известной (как правило, для ее нахождения пишется еще одно уравнение баланса). Ионы образуются в объеме устройства и выпадают на его поверхность. Уравнение баланса при этом запишется

Электроны эмитируются с катода, образуются в объеме в процессе ионизации и выпадают на поверхности устройства. Уравнение баланса при этом записывается так

Энергия вносится в разряд с электронами, эмитированными с катода. Поступающая энергия тратится на ионизацию и уносится с заряженными частицами, выпадающими на стенки устройства. Соответственно, уравнение баланса энергии запишется

К этим уравнениям обычно добавляются эмпирические зависимости «эффективных» сечений столкновения и энергии ионизации от температуры электронов. Полученную систему уравнений решают любым доступным численным методом. В результате находят концентрацию и потенциал плазмы, температуру электронов.

Часто в реальных моделях увеличивают число групп частиц: нейтральные частицы (в том числе на разных уровнях возбуждения), несколько групп электронов, многократно заряженные ионы. Увеличивают число процессов, учитывающихся в модели: например взаимодействие с магнитным полем. Возможно разделение объема реального устройства на несколько областей с различными параметрами плазмы. Пример расчета реального устройства по подобной методике приведен в книге [8].

Источник

Моделирование коэффициентов активности компонентов системы ацетон — пропанол с помощью уравнений Вильсона, NRTL и UNIFAC

Дата публикации: 21.03.2020 2020-03-21

Статья просмотрена: 200 раз

Библиографическое описание:

Остапчук, А. В. Моделирование коэффициентов активности компонентов системы ацетон — пропанол с помощью уравнений Вильсона, NRTL и UNIFAC / А. В. Остапчук. — Текст : непосредственный // Молодой ученый. — 2020. — № 12 (302). — С. 1-7. — URL: https://moluch.ru/archive/302/68216/ (дата обращения: 07.07.2021).

В данной работе описываются способы определения коэффициентов активности изотермической системы ацетон — пропанол с помощью полуэмпирических методов расчёта и с помощью модели UNIFAC.

Физико-химические свойства системы

Основные физико-химические параметры компонентов системы

Ацетон

Пропанол

Температура плавления, °C

Температура кипения, °C

Молярная масса, г/моль

Ацетон — бесцветная подвижная летучая жидкость с характерным резким запахом. Во всех соотношениях смешивается с водой, диэтиловым эфиром, бензолом, метанолом, этанолом, многими сложными эфирами. Органическое вещество, имеющее формулу CH3–C(O)–CH3, простейший представитель насыщенных кетонов.

Пропанол — одноатомный спирт. Встречается в природе в небольших количествах как продукт ферментации. Бесцветная жидкость со спиртовым запахом, смешивается с водой и образует с ней азеотропную смесь. Растворим в этаноле, диэтиловом эфире, ацетоне, бензоле и других органических растворителях.

1) Бинарная система (ацетон — пропанол)

2) Паровая фаза считается идеальной (подчиняется закону Дальтона)

3) Давления насыщенных паров компонентов системы рассчитаны по уравнению Антуана

4) Коэффициенты активности компонентов системы рассчитаны по методу UNIFAC

5) Система изотермическая (25 0 С)

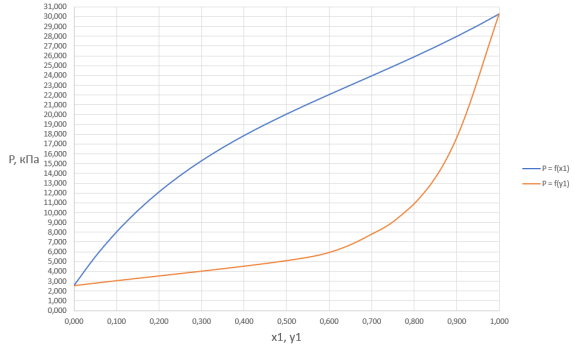
Подставив исходные данные в программу ChemSep, были получены данные о равновесии в системе:

Рис. 1. График зависимости общего давления в системе от содержания ацетона в жидкой и газовой фазах

Составы равновесных фаз для системы ацетон (1) –пропанол (2) при общем давлении Ри температуре 25º C

Температура, 0 С

доля C3H6O

в жидкой фазе

доля C3H6O

в паровой фазе

Общее

давление, кПа

Давление чистого

C3H6O, кПа

Давление чистого

C3H7OH, кПа

В связи с низким общим давлением в системе при заданной температуре и отсутствием сильной ассоциации компонентов в паровой фазе считаем данную паровую систему идеальной. При этом допущении расчет коэффициентов активности компонентов возможен по уравнению:

Где х₁, у₁ — доли ацетона в жидкой и паровой фазах соответственно

Р — общее давление в системе

,− давление чистых ацетона и пропанола соответственно

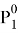
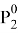
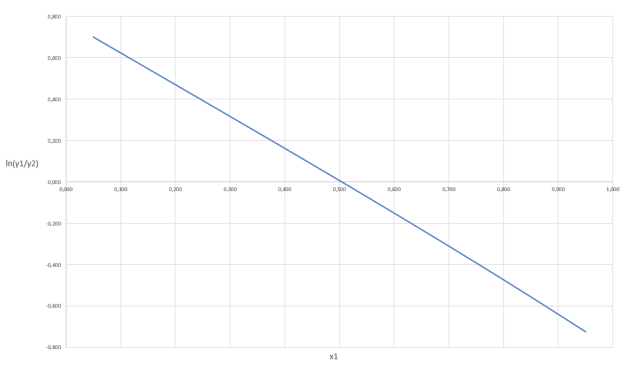
Построив график зависимости ln(γ₁/γ₂) = f(x₁) можем сделать вывод о термодинамической согласованности данных.

Рис. 2. График зависимости логарифма отношения коэффициентов активности от содержания ацетона в жидкой фазе

Так как площадь под графиком равна 0, то система является термодинамически согласованной.

Полуэмпирические модели

В случае полуэмпирических моделей структура модельных уравнений выводится из теории растворов, но обработка экспериментальных данных совершается с использованием регрессионных параметров.

Модель Вильсона

Наибольшее распространение обрела модель «локальных составов». Первое уравнение, образованное на этой модели, было выведено в 1964 г. Вильсоном. Модель «локальных составов» основана на том, что в результате межмолекулярных взаимодействий в смеси начинаются локальные микросоставы, неэквивалентные макросоставу раствора по приготовлению. Разница локальных и средних концентраций компонентов связанна с разностью энергией взаимодействия одноименных и разноименных пар молекул.

Для расчета коэффициентов активности компонентов бинарной системы применяются следующие уравнения:

Где Λ₁₂, Λ₂₁ — приведенные параметры, оцениваемые по экспериментальным данным для данной системы.

Между параметрами уравнения Вильсона и коэффициентами активности компонентов при бесконечном разбавлении получаются следующие зависимости:

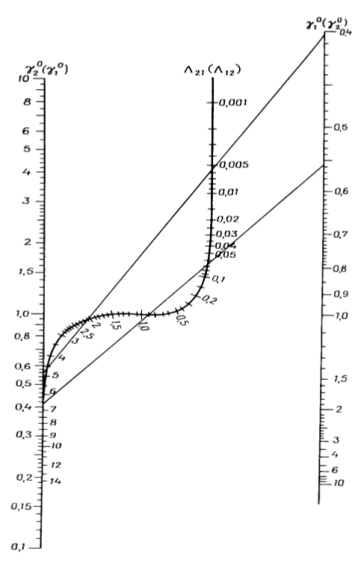
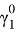
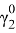
С помощью номограммы определяем начальные значения Λ₁₂ = 0,7, Λ₂₁ = 0,6 при = 2,16, = 2,28 и рассчитываем уточненные значения приведенных параметров.

В итоге получаем вытекающие значения приведенных параметров: Λ₁₂ = 0,693, Λ₂₁ = 0,596. Далее ищем значения β и затем ɣ₁, ɣ₂.

Главный минус модели Вильсона заключается в том, что уравнение, как правило хорошо описывающее равновесие жидкость — пар, непригодно для представления данных о равновесии жидкость — жидкость.

Значительное преимущество уравнения Вильсона в сравнении с эмпирическими уравнениями — способность описания поведения многокомпонентных смесей, если известны приведенные параметры для всех составляющих бинарных систем.

Предложены различные модификации уравнения Вильсона, разрешающие ликвидировать его главный недостаток — плохое описание поведения гетерогенных систем.

Рис. 3. Номограмма для определения приведенных параметров уравнения Вильсона

Модель NRTL

Одна из модификаций была выведена Реноном и Прауснитцем в 1968 г. уравнение NRTL (nonrandom two-liquid). Оно также основано на концепции локальных составов и на теории, согласно которой жидкость имеет ячеистую структуру.

Для бинарной системы:

Приведённые энергетические параметры τ₁₂ и τ₂₁ находим, решив систему уравнений:

Далее находим переменные G₁₂ и G₂₁, характеризующие энергию взаимодействия:

α₁₂ = 0,5 — параметр, характеризующий степень упорядоченности распределения молекул в растворе

Решая системы уравнений, находим значение переменных τ₁₂ = 0,515 и τ₂₁ = 0,372. Далее находим G₁₂ = 0,773 и G₂₁ = 0,83.

Математическая форма уравнений обеспечивает модели NRTL большую гибкость, способность описывать самые различные типы зависимости коэффициентов активности от состава. Сохраняя основные достоинства уравнений Вильсона, уравнения NRTL способны также описывать системы с расслаиванием, благодаря чему их часто используют для расчета равновесий жидкость — жидкость и жидкость — жидкость — пар.

Теоретические модели. Метод UNIFAC

Теоретические модели позволяют рассчитывать коэффициенты активности на основании свойств чистых компонентов.

Метод UNIFAC (universal functional activity coefficient — универсальный функциональный коэффициент активности) был разработан в 1975 году Фреденслундом, Джонсом и Праузницем. Данный метод рассчитывает величины коэффициентов активности на основе концепции группового вклада. Предполагается, что взаимодействия между двумя молекулами являются функцией взаимодействий между группами. Для расчета коэффициентов активности этим групповым методом применяется вариант модели локальных составов UNIQUAC. Уравнение UNIQUAC (UNIversal QUAsi-Chemical equation), совмещает в себе концепцию локального состава с квазихимической решеточной теорией Гуггенгейма — Ставермана. Величины коэффициентов активности γ_i рассматривают как сумму двух вкладов — комбинаторного, обусловленного различиями в размерах и форме молекул, и остаточного, определяемого в основном энергетикой межмолекулярных взаимодействий.

Для расчета коэффициентов активности компонентов бинарной системы при заданной температуре и составе системы молекулы компонентов разбиваются на подгруппы.

Геометрические параметры модели UNIFAC

№группы

По UNIFAC

Группа

R_k

Q_k

Количество групп вмолекуле

Источник