Filosofa.net
Все о философии
Главное Меню
Реклама
Рефераты по философии
Законы науки, способы их открытия и обоснования
4. Динамические и статистические законы
Если основой дихотомического деления законов на теоретические и эмпирические является их различное отношение к опыту, то другая важная их классификация основывается на характере тех предсказаний, которые вытекают из законов. В законах первого типа предсказания носят точно определенный, однозначный характер. Так, если задан закон движения тела и известны его положение и скорость в некоторый момент времени, то по этим данным можно точно определить положение и скорость тела в любой другой момент времени. Законы такого типа в нашей литературе называют динамическими. В зарубежной литературе их чаще всего именуют детерминистическими законами, хотя такое название, как мы увидим ниже, вызывает серьезные возражения.
В законах второго типа, которые получили название статистических, предсказания могут быть сделаны лишь вероятностным образом. В таких законах исследуемое свойство, признак или характеристика относятся не к каждому объекту или индивидууму, а ко всему классу, или популяции в целом. Так, когда говорят, что в данной партии продукции 90% изделий отвечает требованиям стандартов, то это вовсе не означает, что каждое изделие обладает 90% качеством. Само выражение в процентах показывает, что речь здесь идет лишь о некоторой части или пропорции из общего числа изделий, которые соответствуют стандарту. Об отдельном же изделии без дополнительного исследования мы не можем заранее сказать, является оно качественным или нет. Этот элементарный пример достаточно ясно иллюстрирует основную особенность всех статистических законов, предсказания которых относительно отдельных индивидуумов или случаев имеют неопределенный характер. Именно эта неопределенность и заставляет исследователя вводить вероятностные понятия и методы для определения и оценки исхода индивидуальных событий массового случайного типа.
Уже классическая концепция вероятности, нашедшая наиболее полное выражение в трудах П. С. Лапласа, дает возможность оценивать исходы простейших массовых событий случайного характера. В этой концепции вероятность интерпретируется как «отношение числа случаев благоприятствующих к числу всех возможных случаев». При этом, конечно, предполагается, что различные случаи являются равновозможными. Однако такая интерпретация имеет довольно ограниченную область применения. Действительно, равновозможных событий, о которых говорится в вышеприведенном определении вероятности, может просто не быть. Азартные игры, которые исторически явились первой моделью для применения и разработки классической концепции вероятности, специально организованы таким образом, что их исходы являются одинаково возможными, или симметричными. Если, например, игральная кость изготовлена достаточно тщательно, то при ее бросании выпадение любого числа очков от 1 до 6 является одинаково возможным. Поскольку в данном примере имеется шесть равновозможных случаев, благоприятствующим же является какой-то один случай, то его вероятность будет равна 1/6. По такой же схеме подсчитывается вероятность событий, которые можно свести к равновозможным. Иногда это не удается сделать даже в сравнительно простых примерах. Так, если ту же игральную кость изготовить с дефектами, тогда выпадение каждой грани не будет равновозможным. Еще более противоречащими классической концепции являются примеры, взятые из физической, биологической и социальной статистики. Допустим, что вероятность того, что данное вещество из радиоактивного материала будет испускать a-частицу, равна 0,0374. Ясно, что этот результат никак нельзя представить по схеме равновозможных событий. Тогда нам пришлось бы допустить 10000 равновозможных исходов, из них только 374 считались бы благоприятствующими. В действительности же здесь имеются лишь две возможности: либо в следующую секунду вещество испустит частицу, либо нет. Чтобы преодолеть подобные трудности, защитники классической концепции широко использовали так называемый принцип недостаточного основания, или одинакового распределения незнания. Согласно этому принципу, два события считаются равновероятными, если у нас не имеется основания для предположения, что одно из них осуществится скорее, чем другое. Поскольку же в качестве основания зачастую здесь выступало состояние знаний познающего субъекта, то само понятие вероятности лишалось своего объективного значения.
Частотная, статистическая или, как ее иногда называют, эмпирическая концепция вероятности исходит не из наперед заданной, жесткой схемы равновозможных событий, а из действительной оценки частоты появления того или иного события при достаточно большом числе испытаний. В качестве исходного понятия здесь выступает относительная частота появления того или иного признака, характеристики, свойства, которые принято называть событиями в некотором множестве или пространстве событий. Поскольку относительная частота определяется с помощью некоторой эмпирической процедуры, то рассматриваемую вероятность иногда называют еще эмпирической. Это не означает, что само теоретическое понятие вероятности в ее статистической или частотной интерпретации можно определить непосредственно опытным путем. Как мы уже отмечали в предыдущей главе, никакого операционального определения для статистической вероятности дать нельзя, ибо помимо эмпирической процедуры при ее определении мы обращаемся к теоретическим допущениям. В самом деле, осуществив те или иные наблюдения или эксперименты, мы можем точно подсчитать, сколько раз интересующее нас событие встречается в общем числе всех испытаний. Это отношение и будет представлять относительную частоту данного события:
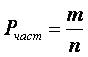
где m означает число появлений данного события, а п — число всех испытаний. Хотя указанное отношение может принимать самые различные численные значения, тем не менее, как показывает практика, для весьма широкого класса случайных массовых событий оно колеблется вокруг некоторого постоянного значения, если число наблюдений или экспериментов будет достаточно велико. Таким образом, тенденция к устойчивости частот обширного класса массовых случайных явлений, обнаруженная на практике, представляет объективную закономерность этих явлений. Абстрактное понятие вероятности как меры возможности наступления события отображает прежде всего этот факт приблизительного равенства относительной частоты вероятности при достаточно большом числе испытаний. Такой подход к вероятности защищается большинством современных специалистов по статистике. Он нашел свое выражение и в широко известном курсе «Математические методы статистики» Г. Крамера. «Всякий раз, — пишет он, — когда мы говорим, что вероятность события Е в эксперименте x равна Р, точный смысл этого утверждения заключается просто в следующем: практически несомненно, что частота события Е в длинном ряду повторений эксперимента x будет приблизительно равной Р. Это утверждение будет называться также частотной интерпретацией вероятности».
Частотный подход к вероятности дает возможность лучше понять специфические особенности статистических закономерностей. Поскольку любое вероятностное утверждение в статистической интерпретации относится не к отдельному событию, а к целому классу однородных или сходных событий, постольку и объяснения и предсказания, полученные с помощью статистических законов, не имеют такого строго однозначного характера, какой присущ динамическим законам. Чрезвычайно важно также отметить, что, в то время как в динамической закономерности необходимость выступает как бы в чистом виде, в статистической закономерности она прокладывает себе дорогу через массу случайностей. В совокупном действии многочисленных случайностей обнаруживается определенная закономерность, которая и отображается статистическим законом.
Как уже отмечалось, статистические закономерности с чисто формальной точки зрения отличаются от закономерностей динамического типа тем, что не определяют значение исследуемой величины достоверным образом, а указывают лишь ее вероятностное распределение. Динамический закон по своей математической форме может быть представлен функциональной связью типа:
 |  |  |  |  |  |  |  |  |  |  |  |  |  |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Название: Законы науки, способы их открытия и обоснования
Дата: 2007-06-09
Просмотрено 42701 раз
Источник
Динамические и статистические законы
Наука исходит из признания того, что все существующее в мире возникает и уничтожается закономерно, в результате дейв ствия определенных причин, что все природные, социальные ипсихические явления связаны между собой причинноследственными связями, а беспричинных явлений не бывает. Такая позиция называется детерминизмом в противоположность индетерминизму, отрицающему объективную причинную обусловленность явлений природы, общества и человеческой психики.
В современной физике идея детерминизма выражается в признании существования объективных физических закономерностей. Открытие этих закономерностей — существенных, повторяющихся связей между предметами и явлениями — задача науки, так же, как и формулирование их в виде законов науки, которые являются нашим знанием о природных закономерностях.
Физика знает два типа физических законов (теорий) — динамические и статистические законы.
Динамический закон — это физический закон, отображающий объективную закономерность в форме однозначной связи физических величин, выражаемых количественно. Динамической теорией является физическая теория, представляющая совокупностьдинамических законов.
Исторически первой и наиболее простой теорией такого рода явилась классическая механика Ньютона. Другими динамическими теориями являются электродинамика Максвелла, механика сплошных сред, термодинамика и общая теория относительности (теория гравитации).
Долгое время считалось, что никаких других законов, кроме динамических, просто не существует. Это было связано с установкой классической науки на механистичность и метафизичность, со стремлением построить любые научные теории по образцу механики Ньютона. Если какие-то объективные процессы и закономерности не вписывались в предусмотренные динамическими законами рамки, не могли быть описаны абсолютно точно посредством определенного набора физических величин, делался вывод о недостатке наших познавательных способностей. Представление о том, что все объективные закономерности должны выражать однозначную связь физических объектов, оставалось незыблемым.
Такая позиция, связанная с отрицанием случайностей любого рода, с абсолютизацией динамических закономерностей и чаконов, называется механическим детерминизмом. Формулирование этого требования в жесткой форме обычно связывают с именем Пьера Лапласа. Согласно провозглашенному Лапласом принципу, все явления в природе предопределены с «железной» необходимостью. Случайному, как объективной категории, нет места в нарисованной Лапласом картине мира. Только ограниченность наших познавательных способностей заставляет рассматривать отдельные события в мире как случайные. В силу этих причин, а также отмечая роль Лапласа, классический механический детерминизм называют еще жестким, или лапласовским, детерминизмом.
Необходимость отказа от классического детерминизма в физике стала очевидной после того, как выяснилось, что динамические законы не универсальны и не единственны. Более того, оказалось, что при описании движения отдельных макроскопических тел, которое всегда считалось сферой действия динамических законов, осуществление идеального классического детерминизма практически невозможно.
В середине XIX в. в физике были сформулированы законы, предсказания которых не являются определенными, а только вероятными. Они получили название статистических законов.
Представление о законах и закономерностях особого типа, которых связи между величинами, входящими в теорию, неодпозначны, впервые ввел Максвелл в 1859 г. при построении статистической механики — первой фундаментальной теории нового типа. Он первым понял, что при рассмотрении систем, состоящих из огромного числа частиц (в данном случае — молекулы газа в сосуде), нужно ставить задачу иначе, чем в механике Ньютона. Для этого Максвелл ввел в физику понятие вероятности, выработанное ранее математиками при анализе случайных явлений, в частности азартных игр.
При бросании игральной кости, как мы знаем, может выпасть любое число очков от 1 до 6. Предсказать, какое число очков выпадет при данном броске кости, нельзя. Мы можем подсчитать лишь вероятность выпадения любого числа очков. В данном случае она будет равна 1/6. Эта вероятность имеет объективный характер, так как выражает объективные отношения реальности. Действительно, если мы бросим кость, какая-то сторона с определенным числом очков выпадет обязательно. Это такая же строгая причинно-следственная связь, как и та, что oтражается динамическими законами, но она имеет другую форму, так как показывает вероятность, а не однозначность события.
Проблема в том, что для обнаружения такого рода закономерностей обычно требуется не единичное событие, а цикл подобных событий. В данном случае мы можем получить статистические средние значения. Так, если бросить кость 300 раз, то среднее число выпадения любого значения будет равно 300 х 1/6 = 50 paз. При этом совершенно безразлично, бросать одну и ту же кость или одновременно бросить 300 одинаковых костей.
Статистические законы, в отличие от динамических законов, отражают однозначную связь не физических величин, а статистическое распределение этих величин. Результат, изменение состояния, которое определяется на основе соответствующих уравнений, также выражается не значениями физических величин, а вероятностями этих значений внутри заданных интервалов. Но это такой же однозначный результат, как и в динамических теориях. Ведь статистические теории, как и динамические теории, выражают необходимые связи в природе, а они не могут быть выражены иначе, чем через однозначную связь состояний. Различается только способ фиксации этих состояний.
На уровне статистических законов и закономерностей мы также сталкиваемся с причинностью. Но это иная, более глубокая форма детерминизма. В отличие от жесткого классического детерминизма он может быть назван вероятностным (современным) детерминизмом. Эти законы меньше огрубляют действительность, имеют менее сильные гносеологические предпосылки, поэтому они способны учитывать и отражать те случайности, которые происходят в мире.
Сегодня любой известный в природе процесс более точно описывается статистическими законами. Но окончательно это стало ясно после создания квантовой механики — статистической теории, описывающей явления атомарного масштаба, то есть движение элементарных частиц и состоящих из них систем. Тогда бьша выяснена принципиальная невозможность динамического описания этих процессов.
Дата добавления: 2016-02-27 ; просмотров: 3484 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник


