Один властелин которому его звездочет наскучил своими ложными предсказаниями решил казнить его

Содержание

задачи на теорию вероятности.
Для просмотра формул ваш браузер должен поддерживать MathML.
задачи на теорию вероятности.
Для просмотра формул ваш браузер должен поддерживать MathML.
задачи на теорию вероятности.
Для просмотра формул ваш браузер должен поддерживать MathML.
МП-2 / БДЗ-1 / Задачи из БДЗ-1

задачи на теорию вероятности.

Для просмотра формул ваш браузер должен поддерживать MathML.

Объявления		Последний пост
	Правила и принципы форума «Высшая математика»	28.10.2009 15:17
	Студенты и преподаватели мехмата МГУ могут бесплатно получать лицензию на Wolfram Mathematica	25.11.2020 00:55
	Tinkoff Business Analyst / Product Owner	19.02.2021 19:06

Доброго времени суток уважаемые математики. Мне очень нужна помощь по решению задач, уже всю голову себе сломал никак не получается. Помогите пожалуйста с решением.
1) На склад поступило 15 кофемолок и 10 кофеварок. Для контроля качества взяли три вещи. Найти вероятность того, что среди взятых а) только одна кофемолка; б) хотя бы одна кофемолка.
2) Один властелин, которому наскучил его звездочет со своими ложными предсказаниями, решил казнить его. Однако, будучи добрым повелителем, он решил дать звездочету последний шанс. Ему велено распределить по двум урнам 4 шара: 2 черных и 2 белых. Палач выберет наугад одну из урн и из нее вытащит один шар. Если шар будет черным, то звездочета казнят, в противном случае, его жизнь будет спасена. Каким образом звездочет должен разместить шары в урнах, чтобы обеспечить себе максимальную вероятность быть спасенным?
3) В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9; для велосипедиста – 0,8 и для бегуна – 0,75. Найти вероятность того, что спортсмен, выполнивший норму – бегун.
4) Произведено 4 выстрела по цели. Вероятность попадания для каждого равна 0,2. Для разрушения достаточно 2 попаданий. Найти вероятность того, что цель будет разрушена.
5) Станок штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей а) ровно 4 будут бракованными; б) бракованных будет меньше четырех

заранее благодарю.Буду крайне признателен если приложите решение!

Источник

задачи на теорию вероятности.

Для просмотра формул ваш браузер должен поддерживать MathML.

Объявления		Последний пост
	Работодателям и кадровым агентствам: Размещение вакансий	26.03.2008 03:07
	Математик-алгоритмист (Vehicle Routing Problem) – удаленная работа	03.06.2020 17:58
	Huawei — Research scientist (math)	22.06.2021 11:25

заранее благодарю.Буду крайне признателен если приложите решение!

Источник

задачи на теорию вероятности.

Для просмотра формул ваш браузер должен поддерживать MathML.

Объявления		Последний пост
	Математик-алгоритмист (Vehicle Routing Problem) – удаленная работа	03.06.2020 17:58
	Преподаватель мехмата МГУ удостоен международной премии по математике Presburger Award	28.07.2020 01:04
	Huawei — Research scientist (math)	22.06.2021 11:25

заранее благодарю.Буду крайне признателен если приложите решение!

Источник

МП-2 / БДЗ-1 / Задачи из БДЗ-1

В специализированную больницу поступают в среднем 50% больных с заболеваниями K 30% — с заболеванием L, 20% — с заболеванием М. Вероятность полного излечения болезни K равна 0,7; для болезней L и М эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что больной страдал заболеванием K.

А – событие, что больной был выписан здоровым.

А1 – гипотеза, что больной страдал заболеванием K.

А2 – гипотеза, что больной страдал заболеванием L.

А3 – гипотеза, что больной страдал заболеванием М.

P(A1) = 0,5; ;

P(A2) = 0,3; ;

P(A3) = 0,2; .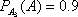

Для решения задачи воспользуемся формулой Байеса, т. к. событие А уже произошло.

В знаменателе этой дроби стоит вероятность P(A), найдем ее отдельно для облегчения вычислений

=0,5*0,7+0,3*0,8+0,2*0,9=0,77

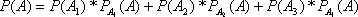
Ответ: вероятность того, что больной страдал заболеванием K, равна .

В первой урне находится один белый и 9 черных шаров, а во второй – один черный и 5 белых шаров. Из каждой урны удалили случайным образом по одному шару, а оставшиеся шары ссыпали в третью (свободную) урну. Найдите вероятность того, что шар, вынутый из третьей урны, окажется белым.

А – событие, что шар, вынутый из третьей урны, белый.

А1 – гипотеза, что удалили оба белых шара.

А2 – гипотеза, что удалили один белый и один черный шар.

А3 – гипотеза, что удалили оба черных шара.

По условию задачи в первой урне изначально было 10 шаров, во второй – 6 шаров. Всего 6 белых и 10 черных шаров. В третьей урне оказалось14 шаров.

;

Подставим эти вероятности в формулу полной вероятности, получим:

Ответ: вероятность того, что шар, вынутый из третьей урны, окажется белым

равна .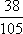

На трех дочерей – Алису, Марину и Елену – в семье возложена обязанность мыть посуду. Поскольку Алиса старшая, ей приходится выполнять 40% всей работы. Остальные 605 работы Марина и Елена делят поровну. Когда Алиса моет посуду, вероятность для нее разбить по крайней мере одну тарелку равна 0,02. Для Марины и Елены эта вероятность равна соответственно 0,03 и 0,04. Родители не знают, кто мыл посуду вечером, но они слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла Алиса? Марина? Елена?

А – событие, что тарелка разбита.

А1 – гипотеза, что посуду мыла Алиса.

А2 – гипотеза, что посуду мыла Марина.

А3 – гипотеза, что посуду мыла Елена.

Для решения задачи воспользуемся формулой Байеса, т. к. событие А уже произошло.

P(A1) = 0,4; ;

P(A2) = 0,3; ;

P(A3) = 0,3; .

Применяя формулу Байеса, получим:

;

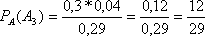
Ответ: вероятность того, что посуду мыла Алиса равна ; вероятность того, что посуду мыла Марина равна ; вероятность того, что посуду мыла Елена равна .

Один властелин, которому наскучил его звездочет со своими ложными предсказаниями, решил казнить его. Однако, будучи добрым повелителем, он решил дать звездочету последний шанс. Ему велено распределить по 2 урнам 4 шара: 2 черных и 2 белых. Палач выберет наугад одну из урн и из нее вытащит один шар. Если шар будет черным, то звездочета казнят, в противном случае его жизнь будет спасена. Каким образом звездочет должен разместить шары в урнах, чтобы обеспечить себе максимальную вероятность быть спасенным?

А – событие, что звездочет спасен.

Рассмотрим 3 случая:

А1 – гипотеза, что палач выберет урну I.

А2 – гипотеза, что палач выберет урну II.

P(A1)= P(A2)=.

Для каждого из трех случаев найдем P(A) по формуле полной вероятности:

1) .

2) или

3) для каждой урны.

Для наглядности приведем значения вероятностей к общему знаменателю:

1) ;

2) ;

3) .

Ответ: чтобы обеспечить себе максимальную вероятность быть спасенным,

звездочет должен разместить шары в урнах способом 2).

При переливании крови надо учитывать группу крови донора и больного. Человеку, имеющему четвертую группу крови, можно перелить кровь любой группы; человеку со второй или третьей группой крови можно перелить кровь либо той же группы, либо первой; человеку с первой группой крови можно перелить только кровь первой группы. Среди населения 33,7% имеют первую, 37,5% — вторую, 20,9% — третью и 7,9% — четвертую группу крови.

а) Найдите вероятность того, что случайно взятому больному можно

перелить кровь случайно взятого донора.

б) Найдите вероятность того, что переливание крови можно осуществить,

если имеются 2 донора.

в) Найдите вероятность того, что переливание крови можно осуществить,

если имеются 3 донора.

А – событие, что случайно взятому больному можно перелить кровь

случайно взятого донора.

А1 – гипотеза, что больной имеет 1 группу крови.

А2 – гипотеза, что больной имеет 2 группу крови.

А3 – гипотеза, что больной имеет 3 группу крови.

А4 – гипотеза, что больной имеет 4 группу крови.

;

Применяя формулу полной вероятности, получаем:

Р(А)=0,337*0,337 + 0,375*0,712 + 0,209*0,546 + 0,079 = 0,11357 + 0,267 +

+ 0,1141 + 0,079 = 0,57368.

А – событие, что переливание крови можно осуществить, если имеются 2

А1 – гипотеза, что больной имеет 1 группу крови.

А2 – гипотеза, что больной имеет 2 группу крови.

А3 – гипотеза, что больной имеет 3 группу крови.

А4 – гипотеза, что больной имеет 4 группу крови.

(для этого достаточно, чтобы хотя бы один их двух доноров имел первую группу крови);

(для этого достаточно, чтобы хотя бы один их двух доноров имел первую или вторую группу крови);

(для этого достаточно, чтобы хотя бы один их двух доноров имел первую или третью группу крови);

Применяя формулу полной вероятности, получаем:

Р(А)=0,337*0,56043 + 0,375*0,9171 + 0,209*0,7939 + 0,079 = 0,18886 +

+ 0,34391 +0,1659 + 0,079 = 0,77768.

А – событие, что переливание крови можно осуществить, если имеются 3

А1 – гипотеза, что больной имеет 1 группу крови.

А2 – гипотеза, что больной имеет 2 группу крови.

А3 – гипотеза, что больной имеет 3 группу крови.

А4 – гипотеза, что больной имеет 4 группу крови.

(для этого достаточно, чтобы хотя бы один их трех доноров имел первую группу крови);

(для этого достаточно, чтобы хотя бы один их трех доноров имел первую или вторую группу крови);

(для этого достаточно, чтобы хотя бы один их трех доноров имел первую или третью группу крови);

Применяя формулу полной вероятности, получаем:

Р(А)=0,337*0,7086 + 0,375*0,9761 + 0,209*0,9064 + 0,079 = 0,2388 +

+ 0,3660 +0,18944 + 0,079 = 0,87271.

Ответ: а) вероятность того, что случайно взятому больному можно

перелить кровь случайно взятого донора, равна 0,57368;

б) вероятность того, что переливание крови можно осуществить,

если имеются 2 донора, равна 0,77768;

в) вероятность того, что переливание крови можно осуществить,

если имеются 3 донора, равна 0,87271.

Пример. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?

Решение. Играют равносильные шахматисты, поэтому вероятность выигрыша р = 1/2; следовательно, вероятность проигрыша q также равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли. Найдем вероятность того, что две партии из четырех будут выиграны:

Р₄ (2)=C₄ 2 p 2 q 2 = 4*3/(1*2)*(1/2) 2 (1/2) 2 = 6/16.

Найдем вероятность того, что будут выиграны три партии из шести:

Так как Р₄(2)> Р₆(3), то вероятнее выиграть две партии из четырех, чем три из шести.

Пример. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй—84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.

Решение. Обозначим через А событие—деталь отличного качества. Можно сделать два предположения (гипотезы): B₁—деталь произведена первым автоматом, причем (поскольку первый автомат производит вдвое больше деталей, чем второй) Р (В₁) =2/3; В₂ — деталь произведена вторым автоматом, причем Р(В₂) = 1/3. Условная вероятность того, что деталь будет отличного каче¬ства, если она произведена первым автоматом, Рв, (Л) =0,6.

Условная вероятность того, что деталь будет отличного качества, если она произведена вторым автоматом, Рв,(А) =0,84. Вероятность того, что наудачу взятая деталь окажется отличного качества, по формуле полной вероятности равна

Искомая вероятность того, что взятая отличная деталь произведена первым автоматом, по формуле Бейеса равна

Источник