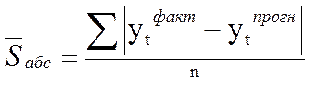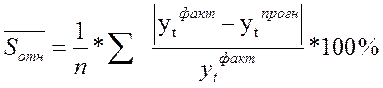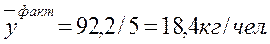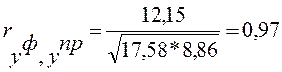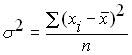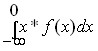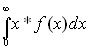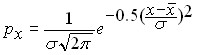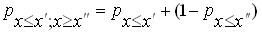Как определить точность предсказания модели

ЛЕКЦИЯ 5. ТОЧНОСТЬ И ДОСТОВЕРНОСТЬ ПРОГНОЗОВ

Важным этапом прогнозирования социально-экономических явлений является оценка точности и достоверности прогнозов.

Точность прогноза тем выше, чем меньше величина ошибки, которая представляет собой разность между прогнозируемым и фактическим значением исследуемой величины.

Вся проблема состоит в том, чтобы вычислить ошибку прогноза, так как фактическое значение прогнозируемой величины станет известно только в будущем. Следовательно, методы оценки точности по уже свершившимся событиям (апостериорные) не имеют практической ценности, так как являются лишь констатацией факта. При разработке прогноза оценку его точности требуется производить заранее (априорно), когда истинное значение прогнозируемой величины еще не известно.

Все показатели оценки точности статистических прогнозов условно можно разделить на три группы:

·Аналитические (абсолютные и относительные);

Аналитические показатели точности прогноза позволяют количественно определить величину ошибки прогноза. К ним относятся следующие показатели точности прогноза:

1) Абсолютная ошибка прогноза (S_абс) определяется как разность между эмпирическим и прогнозным значениями признака и вычисляется по формуле:

где у_t факт – фактическое значение признака;

у_t погн — прогнозное значение признака.

2) Относительная ошибка прогноза (S_отн) может быть определена как отношение абсолютной ошибки прогноза
к фактическому значению признака (у_t)_:

3) Средним показателем точности прогноза является средняя абсолютная ошибка прогноза ( ), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида:

де n – длина временного ряда.

Средняя абсолютная ошибка прогноза показывает обобщенную характеристику степени отклонения фактических и прогнозных значений признака и имеет ту же размерность, что и размерность изучаемого признака.

4) средняя относительная ошибка прогноза:

5) Для оценки точности прогноза используется средняя квадратическая абсолютная ошибка прогноза, определяемая по формуле:

В качестве сравнительного показателя точности прогноза используется коэффициент корреляции между прогнозными и фактическими значениями признака, который определяется по формуле:

6)

Используя данный коэффициент в оценке точности прогноза следует помнить, что коэффициент парной корреляции в силу своей сущности отражает линейное соотношение коррелируемых величин и характеризует лишь взаимосвязь между временным рядом фактических значений и рядом прогнозных значений признаков. И даже если коэффициент корреляции R = 1, то это еще не предполагает полного совпадения фактических и прогнозных оценок, а свидетельствует лишь о наличии линейной зависимости между временными рядами прогнозных и фактических значений признака.

Одним из показателей оценки точности статистических прогнозов является коэффициент несоответствия (КН), который был предложен Г. Тейлом и может рассчитываться:

7)

КН = 0, если имеет место полное совпадение фактических и прогнозных значений признака.

Сравнительная оценка фактических и прогнозных значений потребления кондитерских изделий в год

Год	Фактическое значение потребления конд. изделий в год (кг/чел)	Прогнозное значение потребления конд. изделий в год (кг/чел)	Оценка точности
Sабс	Sотн, %	(у факт -у прогн ) 2
15,9	16,3	-0,4	-2,52	0,16	6,25
17,2	17,3	-0,1	-0,58	0,01	1,44
18,1	18,2	-0,1	-0,55	0,01	0,09
19,8	19,2	0,6	3,03	0,36	1,96
21,2	20,0	1,2	5,66	1,44	7,84
среднее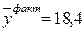
ошибка				КН.=0,336

Решение

Расчет коэффициента корреляции:

				*
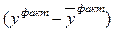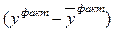-2,5	6,25	-2,1	4,41	5,25
-1,2	1,44	-1,1	1,21	1,32
-0,3	0,09	-0,2	0,04	0,06
1,4	1,96	0,8	0,64	1,12
2,8	7,84	1,6	2,56	4,4
Сумма	17,58	—	8,86	12,15

Линейный коэффициент корреляции изменяется в пределах от -1 до 1: [ ].

Источник

Точность прогнозирования модели в сравнении с интерпретацией в машинном обучении

Дата публикации 2014-08-01

В их книгеПрикладное прогнозное моделированиеКун и Джонсон рано комментируют компромисс между точностью прогнозирования модели и интерпретацией модели.

Для данной проблемы важно иметь четкое представление о том, что является приоритетом, точностью или объяснимостью, чтобы этот компромисс мог быть сделан явно, а не неявно.

В этом посте вы узнаете и рассмотрите этот важный компромисс.

Точность и объяснимость

Производительность модели оценивается с точки зрения ее точности для прогнозирования возникновения события на невидимых данных. Более точная модель рассматривается как более ценная модель.

Интерпретируемость модели позволяет понять взаимосвязь между входными и выходными данными. Интерпретированная модель может ответить на вопросы о том, почему независимые признаки предсказывают зависимый атрибут.

Проблема возникает потому, что с повышением точности модели возрастает сложность модели за счет интерпретируемости.

Сложность модели

Модель с более высокой точностью может означать больше возможностей, выгод, времени или денег для компании. И как таковая точность прогноза оптимизируется.

Оптимизация точности приводит к дальнейшему увеличению сложности моделей в форме дополнительных параметров модели (и ресурсов, необходимых для настройки этих параметров).

«К сожалению, прогнозирующие модели, которые являются наиболее мощными, обычно наименее интерпретируемы.«

Модель с меньшим количеством параметров легче интерпретировать. Это интуитивно понятно. Модель линейной регрессии имеет коэффициент на входную характеристику и член перехвата. Например, вы можете посмотреть на каждый термин и понять, как он влияет на результат. Переход к логистической регрессии дает больше возможностей с точки зрения базовых отношений, которые можно смоделировать за счет преобразования функции в выходные данные, которые теперь также должны быть поняты вместе с коэффициентами.

Дерево решений (скромного размера) может быть понятно, а дерево решений в пакетах требует иной точки зрения для интерпретации того, почему событие прогнозируется. Если двигаться дальше, оптимизированное сочетание нескольких моделей в одном прогнозе может выходить за рамки осмысленной или своевременной интерпретации.

Точность Козыри Объяснимость

В своей книге Кун и Джонсон касаются точности моделей за счет интерпретации.

«Пока сложные модели должным образом проверены, может быть неправильным использовать модель, которая построена для интерпретации, а не прогнозирующей эффективности.«

Интерпретация является вторичной по отношению к точности модели, и они содержат примеры, такие как разграничение электронной почты по спаму и не спаму, а также оценка дома в качестве примеров проблем, когда дело обстоит именно так. Медицинские примеры затрагиваются дважды и в обоих случаях используются для защиты абсолютной потребности и желательности в точности объяснимости, при условии, что модели надлежащим образом проверены.

Я уверен, что «но я подтвердил свою модель» не будет защитой при расследовании, когда модель делает прогнозы, которые приводят к гибели людей. Тем не менее, есть сомнения, что это важный вопрос, который требует тщательного рассмотрения.

Резюме

Всякий раз, когда вы моделируете проблему, вы принимаете решение о компромиссе между точностью модели и ее интерпретацией.

Вы можете использовать знание этого компромисса при выборе методов, которые вы используете для моделирования вашей проблемы и уклонения от ваших целей при представлении результатов.

Источник

Оценка точности прогнозирования случайной величины

Наиболее простой способ охарактеризовать точность прогноза это указать размах колебаний значений случайной величины в выборке. Размах колебаний – это разность между максимальным и минимальными значениями, чем он больше, тем меньше точность прогноза. Но у этой характеристики есть существенный недостаток – при наличии выбросов (аномально больших и аномально малых значений), размах колебаний занижает оценку точности, так как реагирует только на них.

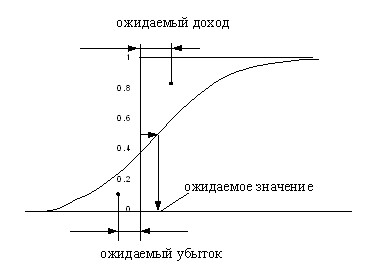
Более объективной характеристикой колеблемости случайной величины должна была бы являться или сумма отклонений случайной величины от своего среднего значения или, что еще лучше, среднее значение этого отклонения. Но в силу того, что отклонения случайной величины от среднего значения могут быть как положительные, так и отрицательные их сумма имеет тенденцию стремиться к нулю. Для устранения этого недостатка необходимо использовать или абсолютные значения этих отклонений или квадраты отклонений. Абсолютные значения представляют меньшие возможности для теоретических построений, по этому исторически сложилось так, что в качестве основного измерителя колеблемости случайной величины используется дисперсия. Дисперсия это средний квадрат отклонения случайной величины от своего среднего значения. Для генеральной совокупности дисперсия определяется по формуле:

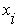
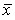
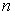
где: – i-е значение из генеральной совокупности случайной величины;

– ее среднее значение;

– число значений случайной величины в генеральной совокупности.

Еще один вариант формулы для расчета дисперсии, удобный при ручном счете или в случае, когда появляются новые значения случайной величины, имеет вид:

.

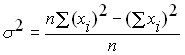
В случае, когда генеральная совокупность не известна, а известна лишь только выборка из нее, то оценка дисперсии генеральной совокупности по данным выборки должна производится по несколько модифицированным формулам:

.

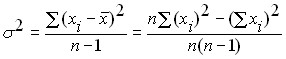
Дисперсия является универсальным показателем степени колеблемости случайной величины, а значит и точности прогноза, но у нее имеется существенный недостаток – это величина по своей сути не имеет единиц измерения (прибыль измеряется в рублях, дисперсия прибыли это рубли в квадрате). 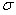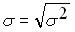По этому наряду с дисперсией для характеристики колеблемости исходных данных используется производная от дисперсии величина – стандартное отклонение (второе название – среднеквадратическое отклонение) , равное корню квадратному от дисперсии, т.е.:

.

В отличии от дисперсии стандартное отклонение имеет туже размерность, что и характеризуемая им случайная величина.

Для полной характеристики точности полученного прогноза одной лишь дисперсии или стандартного отклонения недостаточно, необходимо еще указать тип распределения случайной величины.

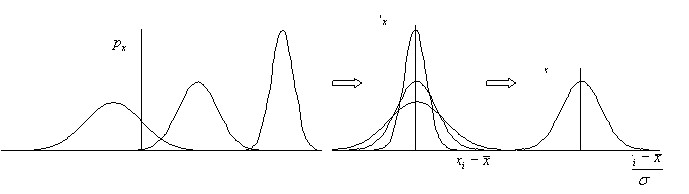
Если взять гистограмму случайной величины и начать увеличивать число интервалов по которым она построена (уменьшать их величину) то гистограмма начнет уменьшаться по высоте и становиться все более гладкой (рис 7). При бесконечно большом числе значений случайной величины и бесконечно малой величине интервалов гистограмма превратится в плавную кривую. Полученная таким образом кривая называется кривой плотности распределения или второе название – функция плотности распределения.

Рис 7. Схема получения кривой плотности распределения.

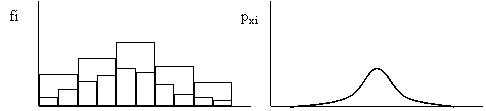
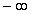
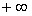
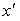
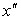
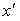
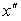
Высота кривой плотности распределения показывает вероятность появления заданного значения случайной величины. Площадь под кривой плотности распределения принимается равной единице. Это вероятность появления любого значения случайной величины в диапазоне от до . Тогда отношение площади фигуры ограниченной кривой плотности распределения и двумя вертикальными отрезками проходящими через и к площади всей фигуры под кривой плотности распределения равно вероятности появления очередного значения случайной величины в диапазоне от до (рис 8, а).

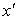
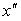
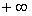
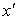
В пределе может быть равно , тогда площадь левой части фигуры будет равна вероятности появления очередного значения случайной величины меньшего или равного (рис 8, б). В случае, когда = , то правая часть фигуры будет равна вероятности появления очередного значения случайной величины большего или равного (рис 8, в).

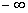
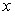
Помимо функции плотности распределения для характеристики типа распределения может использоваться функция, показывающая вероятность появления очередного значения случайной величины меньшего или равного заданному значению. Это кумулятивная (накопленная) функция распределения. Точки на кривой распределения представляют собой значения площади под кривой плотности распределения в диапазоне от до , иными словами они равны интегралу

где: 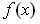– функция плотности распределения.

Рис 8. Использование кривой плотности распределения для определения вероятности появления очередного значения случайной величины в заданном диапазоне.

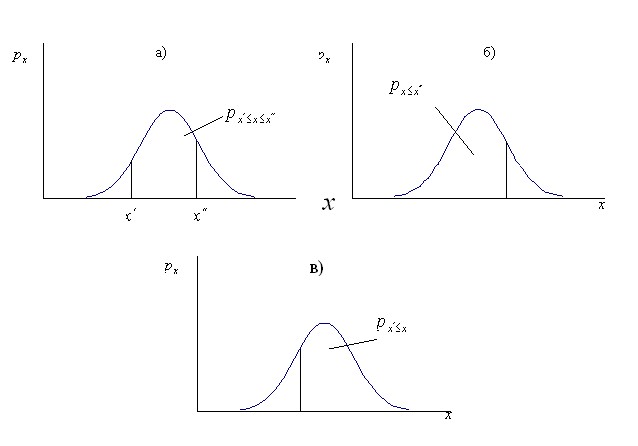
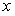
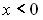
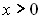
По графику кумулятивной кривой распределения помимо вероятности появления значения случайной величины в заданных пределах, можно определить ее ожидаемое значение (такое , для которого функция распределения равна 0,5), ожидаемый убыток () и ожидаемый доход (). Ожидаемый убыток это расстояние от оси ординат до центра тяжести фигуры, образованной функцией распределения и осями координат. Ожидаемый доход это расстояние от оси ординат до центра тяжести фигуры образованной осью ординат, функцией распределения и горизонтальной прямой, проходящей через 1 на оси ординат (рис.9).

Рис 9. Использования функции распределения для нахождения ожидаемого дохода и убытка.

Математически ожидаемый убыток равен

а ожидаемый доход

Типов распределения случайной величины существует очень много, но наиболее часто встречается на практике нормальное распределение. Его наибольшая распространенность доказана математически. Согласно одному из вариантов предельной теоремы теории вероятности, если исследуемая случайная величина зависит от многих других случайных величин и среди этих влияющих величин нет превалирующих по силе влияния, то исследуемая случайная величина будет иметь распределение близкое к нормальному вне зависимости от того какие распределения имеют влияющие величины.

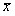
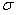
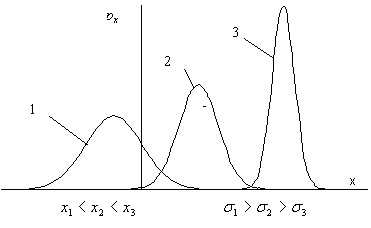
Нормальное распределение имеет форму колоколо-образной симметричной кривой, наивысшая точка которой соответствует , а высота и ширина определяются значением . Функция плотности нормального распределения описывается зависимостью вида:

На рис.10 показаны кривые плотности нормального распределения трех случайных величин, иллюстрирующие влияние параметров случайной величины на кривую плотности нормального распределения. Как следует из этих графиков положение кривой на числовой оси определяется средним значением случайной величины — средина кривой плотности нормального распределения соответствует, а форма кривой – ее высота и ширина — определяются стандартным отклонением .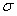

Рис 10. Влияние параметров случайной величины на положение и форму кривой плотности нормального распределения.

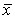
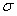
В зависимости от конкретных значений и существует бесчисленное множество вариантов кривой плотности распределения. Тем не менее, за счет алгебраического преобразования случайной величины все это многообразие может быть сведено к одному единственному варианту.

Если вычесть из значений случайной величины ее среднее значение, т.е. осуществить замену координаты на , то все кривые плотности распределения располагаются симметрично оси ординат (рис.11а). Различия между ними сохраняются лишь только в высоте и ширине. Высота каждой из них равна и при становится равной , т.е. случайная величина превращается в обычную детерминированную. Еще одно преобразование заключающееся в делении на стандартное отклонение приводит к тому, что кривые плотности нормального распределений любой случайной величины преобразуется к одной единственной кривой – функции плотности вероятности стандартизованного нормального распределения.

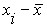
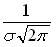
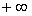
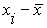
На горизонтальной оси в этом случае откладываются не значения случайной величины, а их безразмерные аналоги, измеренные в стандартных отклонениях.

Рис 11. Преобразование нормального распределения к стандартизованному виду.

Кривая плотности стандартизованного нормального распределения детально изучена. Ее значения, а также значения кумулятивной функции, приводятся практически во всех учебниках по теории вероятности и статистике. Это позволяет легко осуществлять расчеты вероятности появления того или иного события для любой случайной величины имеющей нормальное распределение. 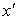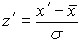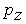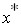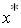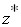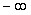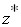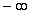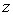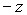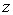Так, например, для определения вероятности появления очередного значения случайной величины, равного необходимо найти , далее по таблице плотности вероятности стандартного нормального распределения найти эту вероятность. В случае, если необходимо найти вероятность того, что очередное значение случайной величины не превысит , то опять необходимо вначале осуществить переход от к и затем искать эту вероятность по таблице появления очередного значения случайной величины в диапазоне от до . Единственная трудность встречающаяся при этом заключается в том, что в различных источниках приводятся различные варианты диапазона для которого осуществлен расчет вероятности появления случайной величины в заданном диапазоне. Этот диапазон может быть в классическом виде от до ; от 0 до , от до . В случае, если расчеты вероятности осуществляются в электронной таблице, то задача существенно упрощается, т.к. в ней имеется специальная функция, позволяющая без использования z — преобразования осуществлять расчет вероятности появления заданного значения случайной величины или того, что она не превысит заданную величину. Все остальные варианты легко находятся согласно схеме рис.6.

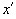
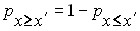
Вероятность того, что очередное значение случайной величины окажется не менее находится по формуле:

,

вероятность того, что очередное значение случайной величины окажется в диапазоне от до — по формуле:

,

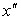
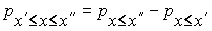
вне этого диапазона:

Для экспрессных оценок вероятности появления того или иного события полезно знать некоторые базовые соотношения для нормального распределения:

вероятность попадания очередного значения случайной величины в интервал

составляет ≈ 68,3%, т.е. шансы примерно 2 к 1

составляет ≈ 95,5 %, т.е. шансы примерно 20 к 1

составляет 99,7%, т.е. шансы примерно 300 к 1.

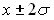
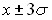
Или иной вариант, более удобный для практики:

существует 10% вероятность того, что очередное значение окажется вне пределов 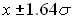(1 шанс из 10);

5% вероятность выхода за пределы (1 шанс из 20);

1% вероятность выхода за пределы 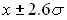(1 шанс из 100).

При работе с выборками всегда возникает вопрос о том насколько обосновано избранное для расчетов то или иное распределение и каковы ошибки при неверно выбранном типе распределения. Русским математиком Чебышевым была доказана теорема о том, что в случае любого распределения вероятность выхода очередного значения за пределы 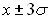не превышает 10%. Иными словами любые ошибки в выборе распределения грозят нам погрешностями не превышающими 10%, в то время как попытки оценок вероятности «на глазок» очевидно чреваты куда более существенными промахами.

В заключение отметим, что задача прогнозирования случайной величины по выборке ее предыдущих значений или по значениям, характерным для объектов того же класса сводится:

к нахождению медианы, среднего значения или моды служащих в качестве прогнозного значения;

указанию пределов и вероятности попадания прогноза в эти пределы в качестве характеристики точности прогноза.

В качестве альтернативного способа характеристики точности прогноза можно указать вероятность получения и ожидаемую величину отрицательного значения прогнозируемой величины и вероятность и ожидаемую величину положительного значения.

Источник