Делаем генеративно-состязательную сеть в Keras и Tensorflow
На предыдущем занятии мы с вами рассмотрели общую концепцию генеративно-состязательных сетей. Теперь, пришло время ее реализовать. Для этого мы воспользуемся пакетом Keras и кое-что сделаем непосредственно через Tensorflow, в частности, раздельный процесс обучения генератора и дискриминатора.
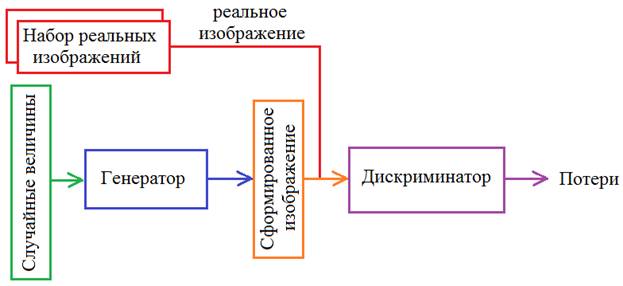
Итак, общая схема генеративно-состязательной сети, будет следующей:
Чтобы генератор лучше формировал изображения, их следует взять однотипными. Например, из базы MNIST выбрать только семерки:
Затем, определим две константы:
и сделаем общую выборку кратную величине BATCH_SIZE:
Стандартизируем входные данные:
И из них формируем тензор реальных изображений, разбитых по батчам:
Обучающая выборка готова. Далее, определим две сети: генератор и дискриминатор. Сделаем их на базе сверточных слоев, так как мы работаем с изображениями, а для них хорошо себя зарекомендовали именно такие сети.
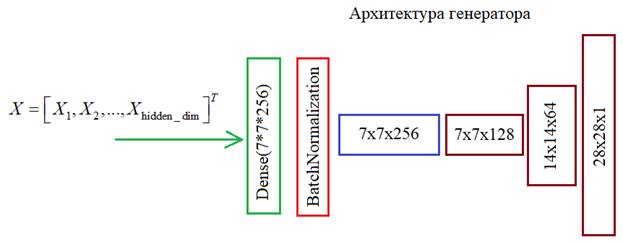
Сеть генератора будет следующей:
Генератор на вход будет получать вектор независимых нормальных СВ, размерностью hidden_dim:
Затем, с помощью слоя Dense он масштабируется до размера 7*7*256 элементов и в слое Reshape преобразуется в тензор с размерами:
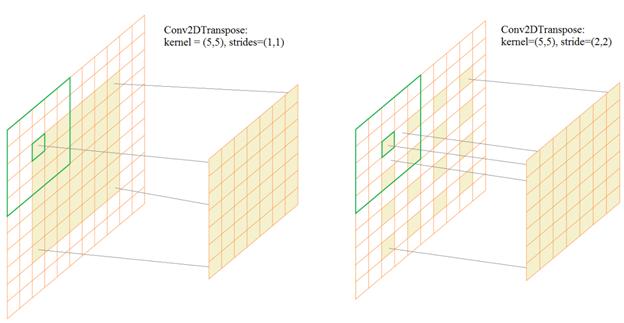
Далее, выполняется операция транспонированной свертки Conv2DTranspose. Принцип ее работы прост и лучше всего виден вот на этом анимированном рисунке
conv2dtranspose — (3,3), (2,2).gif
В частности, у нас происходит следующее. Сначала тензор 7х7х256 преобразуется слоем Conv2DTranspose с ядром 5х5 элементов и шагом (1, 1). На выходе получим те же размеры 7х7, но 128 каналов. Следующий слой Conv2DTranspose имеет ядро 5х5 и шаг (2, 2). Это означает, что входные значения размером 7х7 каждого канала располагаются через отсчет и по ним скользит маска размером 5х5, причем маска смещается на один отсчет. В результате, на выходе получаем размер карт признаков 14х14.
Затем, операция повторяется, также увеличивая размер выходного канала в 2 раза до 28х28. Это и будет результатом работы генератора, то есть, выходное изображение.
Следом определяем сеть дискриминатора:
Здесь все вам уже должно быть знакомо. На входе ожидаем изображение 28х28 пикселей, а на выходе имеем один нейрон с линейной функцией активации. Такая функция выбрана не случайно. Она предотвращает попадание в области насыщения, которые имеются у других функций, например, сигмоидальной или гиперболического тангенса. Линейная функция не ограничивает выходное значение, а значит, не уменьшает результирующие градиенты. Это очень важно при обучении такой сети.
Итак, Сети определены. Дальше мы объявим две функции для вычисления потерь генератора и дискриминатора:
Мы используем встроенную функцию BinaryCrossentropy пакета Keras для вычисления бинарной кросс-энтропии. Далее, в функции generator_loss в бинарной кросс-энтропии передаем два параметра: желаемый и реальный отклики. У генератора желаемый отклик дискриминатора должен быть 
. Именно это мы и указываем первым параметром tf.ones_like(fake_output). А второй – это действительное значение на дискриминаторе. В итоге получаем вычисления по формуле:
По аналогии вычисляются потери для дискриминатора. Ему на вход последовательно будем подавать реальное и фейковое изображения, получать два разных отклика real_output и fake_output и на их основе вычислять потери в соответствии с формулой:
Здесь требуемые отклики равны 
, что и указывается первыми параметрами функции кросс-энтропии.
После определения потерь, зададим оптимизаторы для алгоритма градиентного спуска по Адаму с шагом 0,0001:
Теперь у нас все готово, чтобы сформировать процесс обучения генератора и дискриминатора. Для этого воспользуемся непосредственно средствами Tensorflow 2.0 и определим функцию одного шага обучения через декоратор tf.function:
Давайте разберемся что здесь происходит. На вход функции подаем пакет (батч) реальных изображений. Затем, формируем также один батч вектор нормальных случайных величин длиной hidden_dim. Их мы подаем на вход генератора. Так как нам будут нужны градиенты для сети генератора и дискриминатора, то мы их вычислим с помощью инструмента Tensorflow GradientTape. Он сохраняет необходимые результаты арифметических операции для дальнейшего вычисления градиентов. Это довольно продвинутый инструмент автоматического дифференцирования, о котором можно посмотреть на странице официальной документации:
Я не буду на нем подробно останавливаться, чтобы не перегружать материал, нам здесь важно лишь знать, что объекты gen_tape и disc_tape будут содержать необходимые данные для последующего вычисления градиентов изменяемых параметров (то есть, весов сетей) в точках, соответствующих входным данным.
Благодаря тесной интеграции пакета Keras и Tensorflow, при прохождении сигнала по генератору и дискриминатору:
в объекты gen_tape и disc_tape автоматически записываются необходимые данные. То же самое происходит и при вычислении потерь для обеих сетей.
Теперь, все что нам нужно для вычисления градиентов, это вызвать метод gradient объектов gen_tape и disc_tape. В качестве первого параметра указываем целевую функцию, то есть, функцию потерь, а вторым параметром – оптимизируемые аргументы, от которых зависит эта целевая функция. Конечно, аргументы здесь – это веса соответствующих сетей.
После вычисления градиентов, мы их применяем для изменения весов, используя метод apply_gradients объекта оптимизатора. В качестве параметра передаем список градиентов и оптимизируемых весовых коэффициентов. Это и есть момент обучения сети. Делаем это независимо для генератора и дискриминатора.
В конце, возвращаем значения потерь для генератора и дискриминатора.
Это функция для выполнения одного шага обучения по батчу. Теперь, объявим функцию, которая будет запускать весь процесс обучения сетей. На ее вход будем передавать обучаемую выборку изображений, разбитой по батчам и число эпох:
Здесь все достаточно просто. Вначале определяем вспомогательные переменные. И, затем, делаем цикл по эпохам. Для каждой эпохи замеряем время ее выполнения и запускаем цикл обучения по батчам, вызывая функцию train_step. Далее, вычисляем средние потери для генератора по батчам и выводим результат в консоль, а также сохраняем в коллекции history. В конце возвращаем историю изменения потерь для генератора.
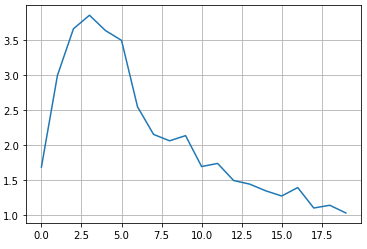
Наконец, запускаем процесс обучения и отображаем график изменения потерь для генератора по эпохам:
Смотрите, здесь наблюдается некоторый колебательный процесс. И это естественно. Сначала происходит резкое увеличение потерь из-за преимущественного обучения дискриминатора (он учится отличать реальные изображения от фейковых). Затем, немного обучившись, градиенты для генератора стали больше градиентов дискриминатора и потери генератора стали уменьшаться (изображения на его выходе становятся реалистичнее). Далее, опять видим небольшие всплески – это моменты улучшения дискриминатора и в целом все это доходит до некоторого равновесного состояния. В идеале, генератор должен выдавать изображения неотличимые от реальных и дискриминатор с вероятностью 0,5 может их различать, то есть, не различать вовсе.
Давайте теперь посмотрим, что выдает генератор после 20 эпох обучения:
Как видим, получаются вполне четкие не смазанные изображения семерок. Это как раз то, к чему мы стремились. Теперь, обученный генератор можно использовать отдельно для формирования таких изображений.
Генеративно-состязательные сети, как правило, долго обучаются в сравнении с обычными сетями. Здесь нам приходится подстраивать весовые коэффициенты отдельно для дискриминатора, затем для генератора и это конкурирующее обучение необходимо повторять много раз для достижения приемлемых результатов. Поэтому число эпох может достигать 100 и более. Дополнительные сложности при обучении возникают из-за взаимного влияния дискриминатора и генератора друг на друга. Вполне может возникнуть ситуация, когда градиенты генератора будут близки к нулю и обучение попадает в некую ловушку, когда недообученный дискриминатор хорошо различает фейковые изображения недообученного генератора. При этом, генератор дальше не обучается из-за этих малых градиентов. Но все это можно преодолеть при грамотном подходе к обучению.
Вот так можно в самом простом случае реализовать и обучить генеративно-состязательную сеть для формирования реалистичных изображений цифр.
Видео по теме
Нейронные сети: краткая история триумфа
Структура и принцип работы полносвязных нейронных сетей | #1 нейросети на Python
Персептрон — возможности классификации образов, задача XOR | #2 нейросети на Python
Back propagation — алгоритм обучения по методу обратного распространения | #3 нейросети на Python
Ускорение обучения, начальные веса, стандартизация, подготовка выборки | #4 нейросети на Python
Переобучение — что это и как этого избежать, критерии останова обучения | #5 нейросети на Python
Функции активации, критерии качества работы НС | #6 нейросети на Python
Keras — установка и первое знакомство | #7 нейросети на Python
Keras — обучение сети распознаванию рукописных цифр | #8 нейросети на Python
Как нейронная сеть распознает цифры | #9 нейросети на Python
Оптимизаторы в Keras, формирование выборки валидации | #10 нейросети на Python
Dropout — метод борьбы с переобучением нейронной сети | #11 нейросети на Python
Batch Normalization (батч-нормализация) что это такое? | #12 нейросети на Python
Как работают сверточные нейронные сети | #13 нейросети на Python
Делаем сверточную нейронную сеть в Keras | #14 нейросети на Python
Примеры архитектур сверточных сетей VGG-16 и VGG-19 | #15 нейросети на Python
Теория стилизации изображений (Neural Style Transfer) | #16 нейросети на Python
Делаем перенос стилей изображений с помощью Keras и Tensorflow | #17 нейросети на Python
Как нейронная сеть раскрашивает изображения | #18 нейросети на Python
Введение в рекуррентные нейронные сети | #19 нейросети на Python
Как рекуррентная нейронная сеть прогнозирует символы | #20 нейросети на Python
Делаем прогноз слов рекуррентной сетью Embedding слой | #21 нейросети на Python
Как работают RNN. Глубокие рекуррентные нейросети | #22 нейросети на Python
LSTM — долгая краткосрочная память | #23 нейросети на Python
Как делать сентимент-анализ рекуррентной LSTM сетью | #24 нейросети на Python
Рекуррентные блоки GRU. Пример их реализации в задаче сентимент-анализа | #25 нейросети на Python
Двунаправленные (bidirectional) рекуррентные нейронные сети | #26 нейросети на Python
Автоэнкодеры. Что это и как работают | #27 нейросети на Python
Вариационные автоэнкодеры (VAE). Что это такое? | #28 нейросети на Python
Делаем вариационный автоэнкодер (VAE) в Keras | #29 нейросети на Python
Расширенный вариационный автоэнкодер (CVAE) | #30 нейросети на Python
Что такое генеративно-состязательные сети (GAN) | #31 нейросети на Python
Делаем генеративно-состязательную сеть в Keras и Tensorflow | #32 нейросети на Python
© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта
Источник
